在MacBook Pro 2019上优化GEMM

Technical 31 minutes read (About 4607 words)

how-to-optimiza-gemm 是大家参考得比较多的gemm优化tutorial，本文是在我的MacBook Pro 2019上进行的实践，处理器型号是i5-8257U.

代码在：https://github.com/LeiWang1999/optimize-gemm-on-macbook2019

1.浮点峰值计算

获取MacBook的CPU信息：

1
2
❯ sysctl machdep.cpu.brand_string
machdep.cpu.brand_string: Intel(R) Core(TM) i5-8257U CPU @ 1.40GHz

得到CPU的型号是i5-8257U，Google一下找到他的Product页面。

首先关注一下Specfication，该CPU一共有四个核，八个线程，但是因为Intel的超线程技术（就是一个核当作两个核来用，我们这种两个线程都吃慢计算单元资源的程序吃不到这个超线程的福利，所以理论上两个线程的吞吐量和四个线程应该是一样的，所以GFLOPS要以四个线程来算）；这里的Boost Technology是指Intel的睿频技术，是指在程序对CPU的资源利用增加时会主动提升CPU运行的频率，并且在睿频加速期间，处理器的温度，功率等超过限制，则会处理器的时钟频率会下降，以保护处理器。

我们在这里不关注睿频的频率，关注处理器的Base频率也就是1.4Ghz。

image-20220212173146231

其次，关注CPU支持的向量指令集（就是说一个指令可以操作向量，即很多个标量被一起操作，比如数组的乘法与加法），对于i5-8257U来说，其支持的扩展指令如下：
image-20220212191541540

关于CPU支持什么样的指令，也可以通过CPU_ID这个指令来检查，在代码里这样写，关于指令和CPUID的简单用法，可以参考这篇文章：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
static void cpuid_x86_exec(struct cpuid_t *cpuid) {
    asm volatile("pushq %%rbx\n"
                 "cpuid\n"
                 "movl %%ebx, %1\n"
                 "popq %%rbx\n"
                 : "=a"(cpuid->eax), "=r"(cpuid->ebx), "=c"(cpuid->ecx), "=d"(cpuid->edx)
                 : "a"(cpuid->ieax), "c"(cpuid->iecx)
                 : "cc");
}

    struct cpuid_t cpuid;

    feat = 0;

    cpuid.ieax = 0x1;
    cpuid.iecx = 0x0;
    cpuid_x86_exec(&cpuid);

    if (BIT_TEST(cpuid.edx, 25)) {
        SET_FEAT(_CPUID_X86_SSE_);
    }
    if (BIT_TEST(cpuid.ecx, 28)) {
        SET_FEAT(_CPUID_X86_AVX_);
    }
    if (BIT_TEST(cpuid.ecx, 12)) {
        SET_FEAT(_CPUID_X86_FMA_);
    }

    cpuid.ieax = 0x7;
    cpuid.iecx = 0x0;
    cpuid_x86_exec(&cpuid);

    if (BIT_TEST(cpuid.ebx, 16)) {
        SET_FEAT(_CPUID_X86_AVX512F_);
    }
    if (BIT_TEST(cpuid.ecx, 11)) {
        SET_FEAT(_CPUID_X86_AVX512_VNNI_);
    }

这样，就可以在程序中获得当前的X86 CPU支持的指令集，并分别调用不通的程序来运算，跑了一下这个程序发现他是支持FMA、AVX、SSE的。

为了计算浮点峰值还需要一个参数就是同一时间段能够处理多少个浮点计算指令，这需要研究一下处理器的微结构，但是我在官方的datasheet里没找到有关的描述。在果壳的体系结构课上领悟到的查chip的各种参数与他们之间的各种联系，还是去wikichip这个网站。

找到wikichip里关于i5-8250U的描述页面：https://en.wikichip.org/wiki/intel/core_i5/i5-8250u

我们的8257和这个8250在微架构上是一样的。

关于intel的命名规则：

第一位代表第几代CPU，一般越大，架构更优。i7-4770K>i7-3770K

第二位代表处理器等级，数字越大，性能越好。i7-4810mq>i7-4710mq

第三位代表核显，可忽略不比

第四位代表功耗可忽略不比

H，M,U，表示功耗，字母越小，功耗越大，性能越好。所以后缀：H>M>U。比如：i5-5350H>i7-4610m,i5-4330m>i7-4558U

在页面描述上可以看到其微结构属于Kaby Lake！再进Kaby Lake的Wiki页面，可以看到单核的微结构图：

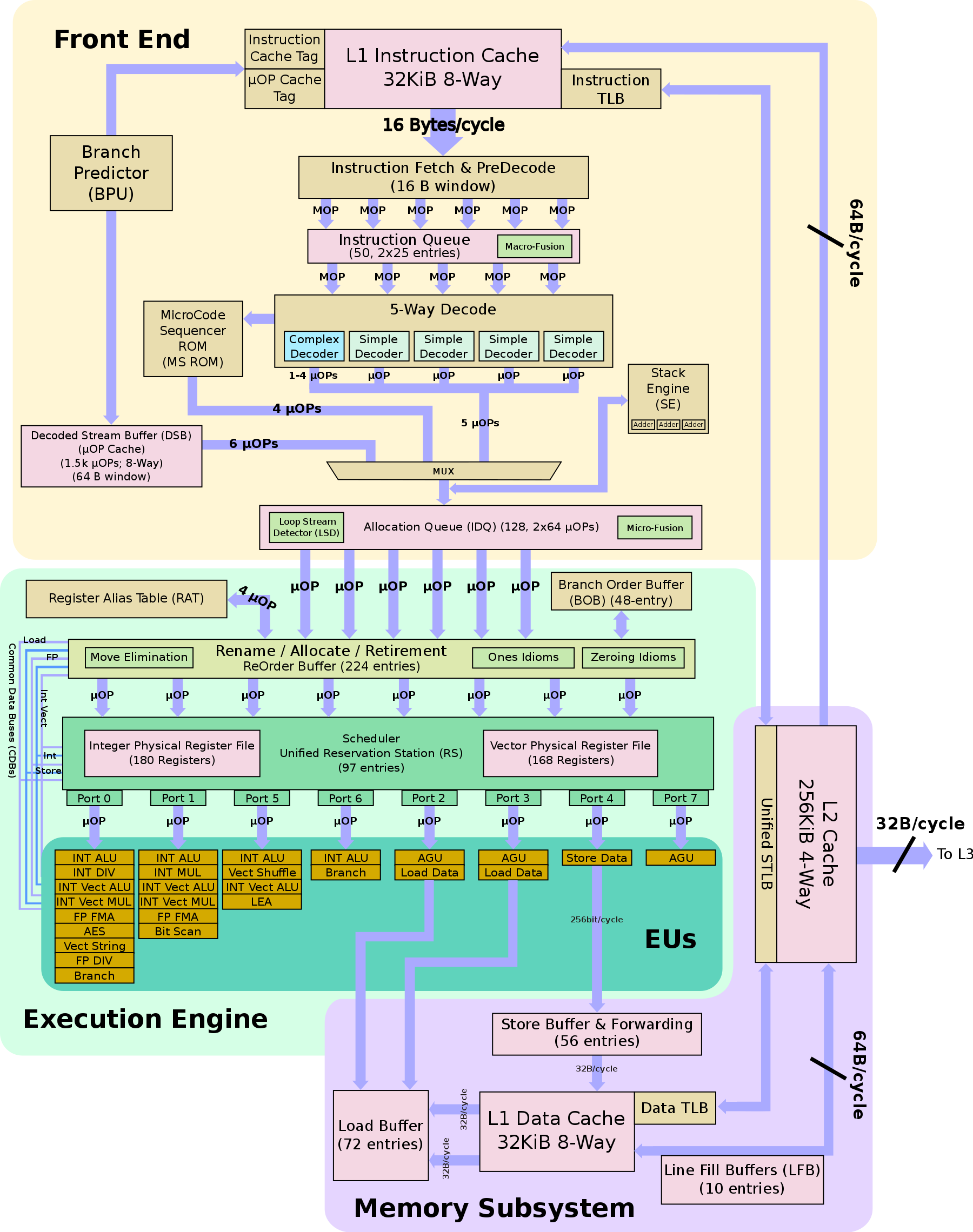
skylake block diagram.svg

PORT0和PORT1可以同时执行向量乘、向量加和FMA指令，通过查datasheet可以知道：

FMA指令集（floating-point fused multiply add）就是256位的融合乘加指令，对于32位的数据来说一个指令可以操作8个操作数，对于64位的数据来说，一个指令可以操作4个操作数，那么对于fp32的数据来说，我们的单核浮点峰值就是：
$$
2(256/32)2*1.4=44.8 \quad GFLOPS
$$
第一个2是两个port、第二个是操作数位fp32的时候的操作数个数，第三个2是乘法和加法两个运算，第三个1.4是没有睿频时的工作频率。

Mac上需要使用到 Turbo Boost Switcher Pro这个软件来关闭睿频，不过我的mbp2019日常开启睿频，风扇疯狂起飞XDD

如果开启了睿频，那么单核浮点峰值就是：
$$
2(256/32)2*3.9=124.8 \quad GFLOPS
$$
实际编写程序测试最大峰值：

1
gemm-optimizer/cmake-build-debug/tools/calc-cpu-flops 4

这里，分别对几个向量指令编写了测试的汇编程序：

1
2
3
4
5
6
7
8
9
10
11
12
❯ tree
.
├── CMakeLists.txt
├── calc-cpu-flops.c
├── cpufp_kernel_x86.h
├── cpufp_kernel_x86_avx.s
├── cpufp_kernel_x86_avx512_vnni.s
├── cpufp_kernel_x86_avx512f.s
├── cpufp_kernel_x86_fma.s
├── cpufp_kernel_x86_sse.s
├── smtl.c
└── smtl.h

关于汇编程序的内容，看一下之前分析的fma的程式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
_cpufp_kernel_x86_fma_fp32:
    mov $0x40000000, %rax
    vxorps %ymm0, %ymm0, %ymm0
    vxorps %ymm1, %ymm1, %ymm1
    vxorps %ymm2, %ymm2, %ymm2
    vxorps %ymm3, %ymm3, %ymm3
    vxorps %ymm4, %ymm4, %ymm4
    vxorps %ymm5, %ymm5, %ymm5
    vxorps %ymm6, %ymm6, %ymm6
    vxorps %ymm7, %ymm7, %ymm7
    vxorps %ymm8, %ymm8, %ymm8
    vxorps %ymm9, %ymm9, %ymm9
._cpufp.x86.fma.fp32.L1:
    vfmadd231ps %ymm0, %ymm0, %ymm0
    vfmadd231ps %ymm1, %ymm1, %ymm1
    vfmadd231ps %ymm2, %ymm2, %ymm2
    vfmadd231ps %ymm3, %ymm3, %ymm3
    vfmadd231ps %ymm4, %ymm4, %ymm4
    vfmadd231ps %ymm5, %ymm5, %ymm5
    vfmadd231ps %ymm6, %ymm6, %ymm6
    vfmadd231ps %ymm7, %ymm7, %ymm7
    vfmadd231ps %ymm8, %ymm8, %ymm8
    vfmadd231ps %ymm9, %ymm9, %ymm9
    sub $0x1, %rax
    jne ._cpufp.x86.fma.fp32.L1
    ret

rax存储的是循环的次数，循环初始化的时候执行的一系列异或指令是用来快速将寄存器的内容置零，接着循环内会执行十次乘累加运算，一共执行40000000次，之前分析得，对于32位的浮点数， 一次乘累加运算可以操作8个数，一共是 40000000 * 8 * 10 * 2（乘法和加法）运算，共这么大的浮点运算量：

1
2
3
#ifdef _FMA_
#define FMA_FP32_COMP (0x40000000L * 160)
#define FMA_FP64_COMP (0x40000000L * 80)

则gflops的计算如下式：

1
perf = FMA_FP64_COMP * num_threads / time_used * 1e-9;

这里有个容易忽略的点，在MacOS上，C/CPP 调用汇编的约定是要在汇编函数前面加个下划线，这样才能对C程序可见，大坑！

因为mac上运行的程序有点多，所以这里的运算一般是吃不满cpu的资源的，我在这里给一下单核睿频关闭情况下跑出来的perf，这将作为我们调优的目标：

1
2
3
4
5
6
7
8
9
10
Thread(s): 1
binding to core 0
fma fp32 perf: 40.9189 gflops.
fma fp64 perf: 22.0921 gflops.
binding to core 0
avx fp32 perf: 21.9944 gflops.
avx fp64 perf: 11.0741 gflops.
binding to core 0
sse fp32 perf: 10.8526 gfops.
sse fp64 perf: 5.4786 gflops.

之前手算单核FMA的GFLOPS是44.8，差的也不是很多，基本上算是正确了。

开个睿频：

1
2
3
4
5
6
7
8
9
10
Thread(s): 1
binding to core 0
fma fp32 perf: 117.0210 gflops.
fma fp64 perf: 58.4361 gflops.
binding to core 0
avx fp32 perf: 56.1949 gflops.
avx fp64 perf: 28.9646 gflops.
binding to core 0
sse fp32 perf: 29.1122 gflops.
sse fp64 perf: 14.6471 gflops.

也和计算的结果差不多。

2.baseline

首先，我们写一个最傻瓜的gemm来作为我们的baseline:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void AddDot( int k, double *x, int incx,  double *y, double *gamma )
{
    /* compute gamma := x' * y + gamma with vectors x and y of length n.

       Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1.
    */

    int p;

    for ( p=0; p<k; p++ ){
        *gamma += X( p ) * y[ p ];
    }
}

/* Routine for computing C = A * B + C */

void mMultBaseLine( int m, int n, int k, double *a, int lda,
               double *b, int ldb,
               double *c, int ldc )
{
    int i, j, p;

    for ( i=0; i<m; i++ ){        /* Loop over the rows of C */
        for ( j=0; j<n; j++ ){        /* Loop over the columns of C */
            AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) );
        }
    }
}

为了方便演示循环展开，这个tutorial把inner product封装成了一个addDot程序，在benchmark程序中，将两个矩阵的尺寸分别从100不断提升到1500，观察矩阵乘法的gflops变化：

1
2
3
#define PFIRST 100
#define PLAST 1500
#define PINC 100

程序运行结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
100 7.299270e-01 0.000000e+00 
200 6.892096e-01 0.000000e+00 
300 6.828183e-01 0.000000e+00 
400 6.939813e-01 0.000000e+00 
500 6.374153e-01 0.000000e+00 
600 6.188340e-01 0.000000e+00 
700 5.687877e-01 0.000000e+00 
800 5.626816e-01 0.000000e+00 
900 5.218054e-01 0.000000e+00 
1000 5.200376e-01 0.000000e+00 
1100 4.751246e-01 0.000000e+00 
1200 4.499168e-01 0.000000e+00 
1300 4.366850e-01 0.000000e+00 
1400 4.270737e-01 0.000000e+00 
1500 3.929416e-01 0.000000e+00

在tools/plot下我提供了一个py程序，用来绘制benckmark的：

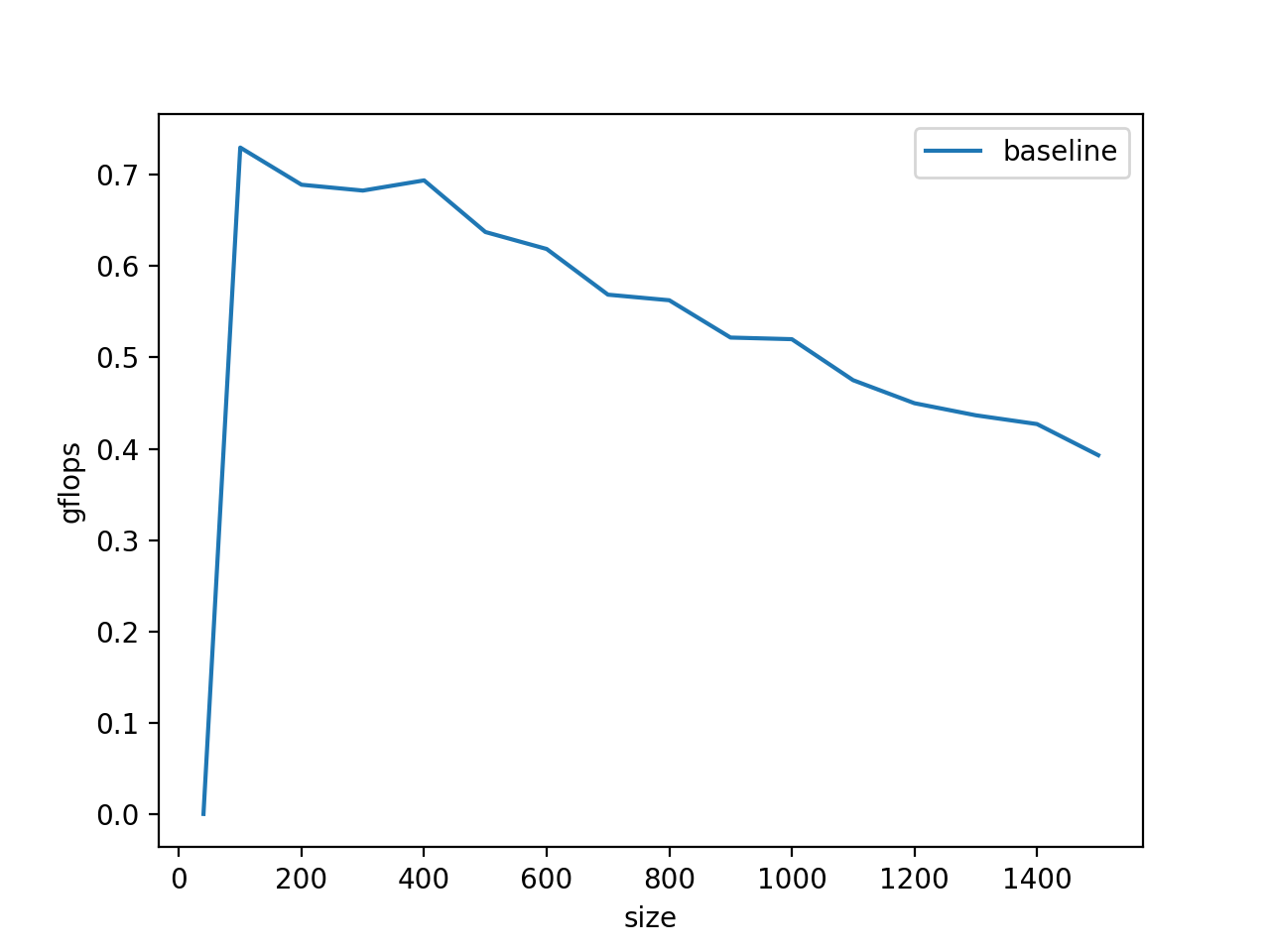baselinegflops只有0.6，并且显而易见在gemm的尺寸变大的时候，gflop有下降趋势，这是因为当运算过程中的矩阵A、B的大小超过了L2 Cache的大小(256Kb)的时候，频繁访问A、B就会导致Cache要重复的访问DDR，变成访存的瓶颈，这部分可以通过矩阵分块计算来解决。

3.循环展开和合并

我们先从最简单的循环展开和合并来观察矩阵的运算，所谓循环展开，是一种通过牺牲程序大小换取效率的方法，比如对上面的gemm程序，循环展开是这样写的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
        /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
     one routine (four inner products) */
      AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) );
      AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) );
      AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) );
      AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) );
    }
  }
}

这样，循环每次结束的时候需要做的j++的次数缩短到了原来的1/4，但是显而易见这对我们的程序性能影响并不大，因为省下来的这点计算量和循环内部的计算相比差别不大，如果循环里面的运算比较简单这样展开还是可以取得不错的效果的，其次，也可以方便硬件做指令重排消除阻塞。

如果我们对AddDot做inline，代码会变成下面这个样子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void MY_MMult( int m, int n, int k, double *a, int lda, 
                                    double *b, int ldb,
                                    double *c, int ldc )
{
  int i, j;

  for ( j=0; j<n; j+=4 ){        /* Loop over the columns of C, unrolled by 4 */
    for ( i=0; i<m; i+=1 ){        /* Loop over the rows of C */
      int p;

   		//  AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) );
      for ( p=0; p<k; p++ ){
        C( 0, 0 ) += A( 0, p ) * B( p, 0 );     
      }

      //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) );
      for ( p=0; p<k; p++ ){
        C( 0, 1 ) += A( 0, p ) * B( p, 1 );     
      }

      //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) );
      for ( p=0; p<k; p++ ){
        C( 0, 2 ) += A( 0, p ) * B( p, 2 );     
      }

      //  AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) );
      for ( p=0; p<k; p++ ){
        C( 0, 3 ) += A( 0, p ) * B( p, 3 );     
      }
    }
  }
}

显然在这里的代码，可以进行循环合并，像下面这样：

1
2
3
4
5
6
for ( p=0; p<k; p++ ){
  C( 0, 0 ) += A( 0, p ) * B( p, 0 );     
  C( 0, 1 ) += A( 0, p ) * B( p, 1 );     
  C( 0, 2 ) += A( 0, p ) * B( p, 2 );     
  C( 0, 3 ) += A( 0, p ) * B( p, 3 );     
}

这样，不仅将循环中for循环的数量缩短了四分之三，也能更好的利用循环的A和B的空间一致性，并且这样基于常数的偏址也会相比基于j+1\j+2这种格式的表达式减少一些运算量，则程序优化之后的benchmark长这样：

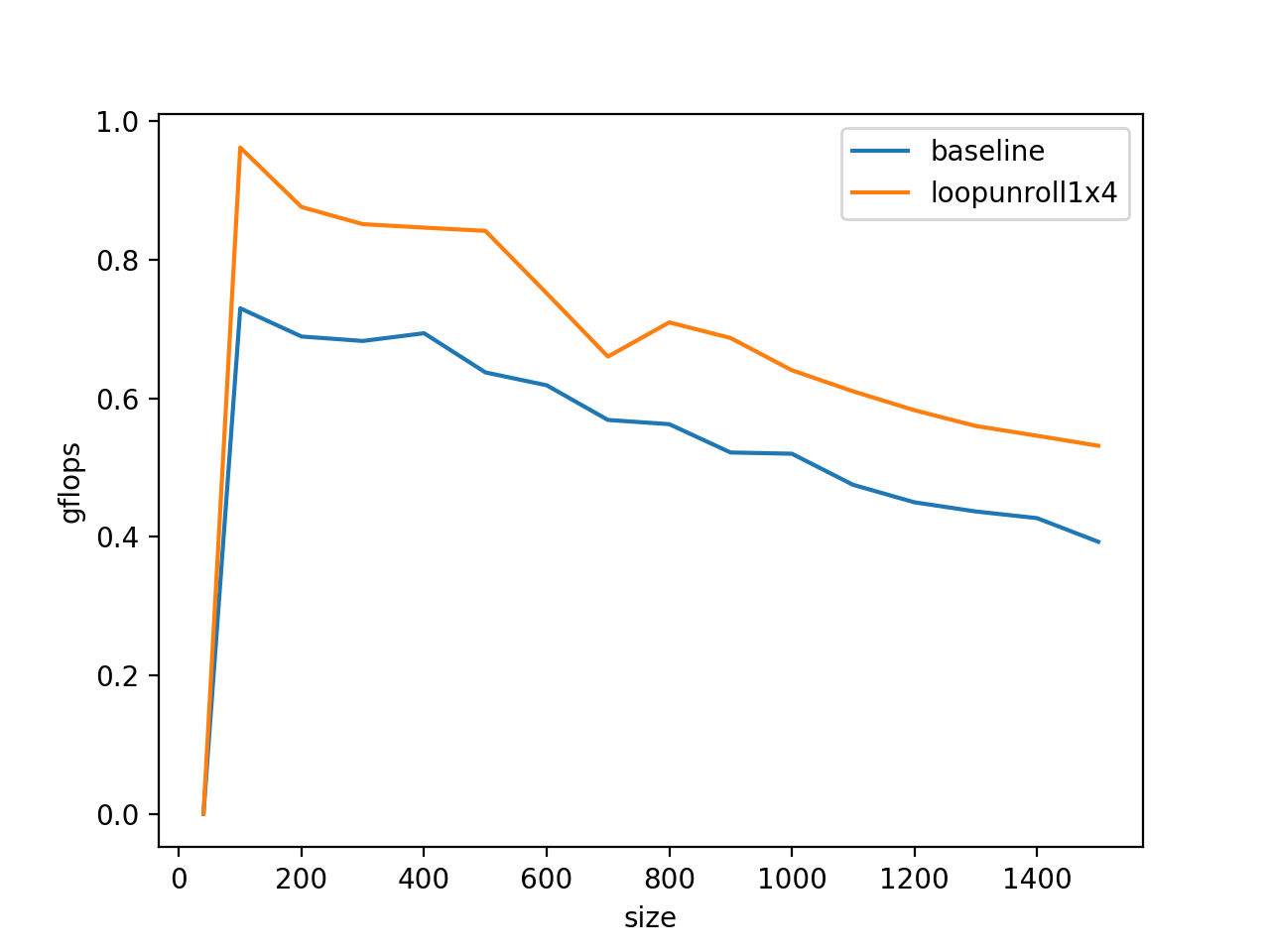
loopunroll1x4

4.访存方式

观察这个循环：

1
2
3
4
5
6
for ( p=0; p<k; p++ ){
  C( 0, 0 ) += A( 0, p ) * B( p, 0 );     
  C( 0, 1 ) += A( 0, p ) * B( p, 1 );     
  C( 0, 2 ) += A( 0, p ) * B( p, 2 );     
  C( 0, 3 ) += A( 0, p ) * B( p, 3 );     
}

C(0,0)被复用了k次，A(0,p)被复用了4次，所以我们将它们放在访问比较快的单元里会有利于程序的性能，在C语言里，使用register将变量塞到物理寄存器里去：

1
2
3
4
5
6
7
8
for ( p=0; p<k; p++ ){
    a_0p_reg = A( 0, p );

    c_00_reg += a_0p_reg * *bp0_pntr++;
    c_01_reg += a_0p_reg * *bp1_pntr++;
    c_02_reg += a_0p_reg * *bp2_pntr++;
    c_03_reg += a_0p_reg * *bp3_pntr++;
}

这里，我们还将B的索引进行了优化：

1
2
3
4
bp0_pntr = &B( 0, 0 );
bp1_pntr = &B( 0, 1 );
bp2_pntr = &B( 0, 2 );
bp3_pntr = &B( 0, 3 );

因为对于原来B的索引，需要计算一个比较复杂的表达式：

1
2
3
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]

这相当于一个循环不变量的外提，减少了计算量，经过这么折腾之后的benchmark：

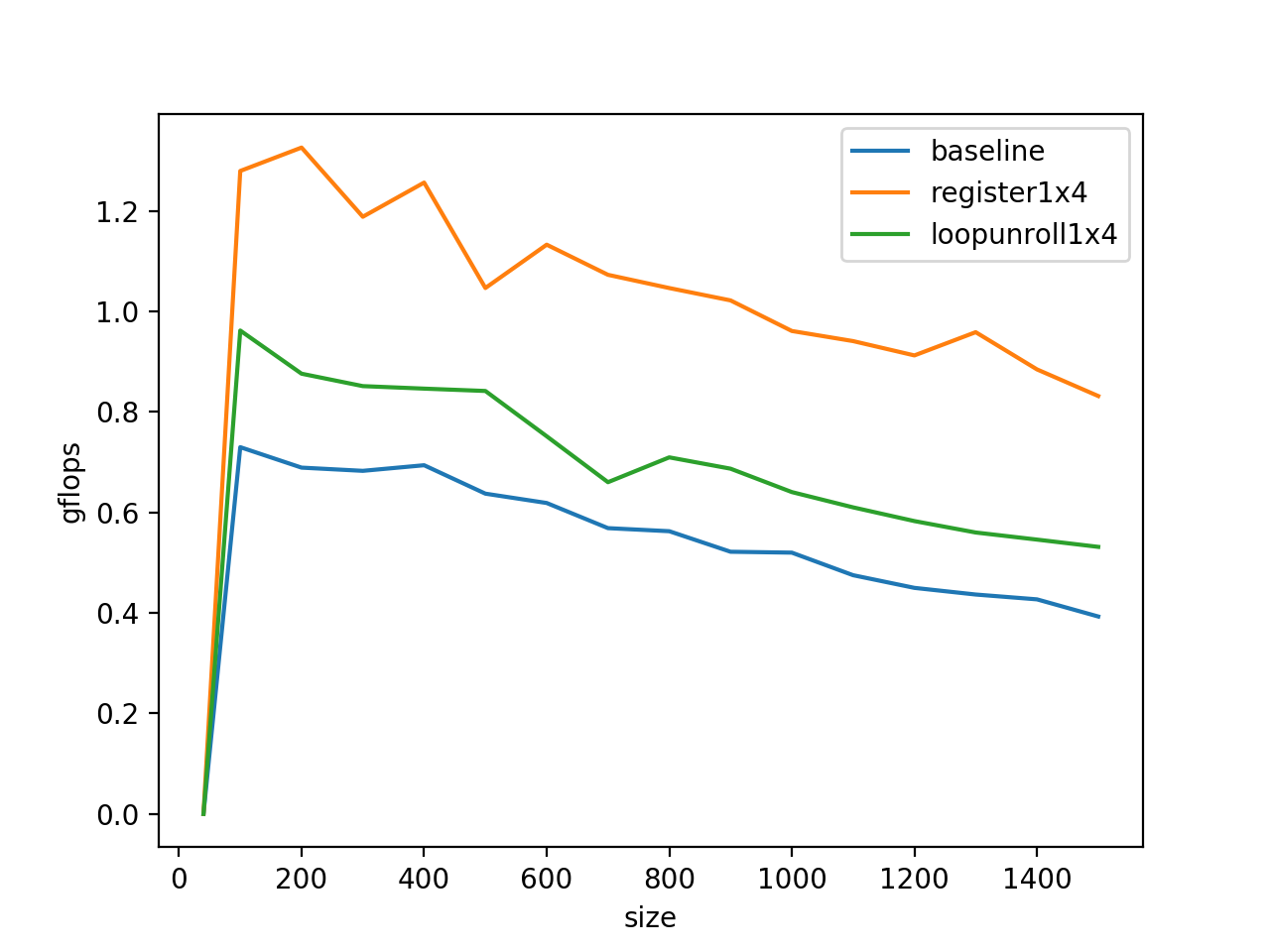
register1x4

5.SIMD指令加速

一个SSE指令可以同时执行两个乘累加运算，在执行乘累加运算之前，需要提前把数据塞到对应的向量寄存器里，这样的向量寄存器共有16个，每个寄存器可以存放两个double数，所以一共可以存放32个double类型的变量，要想达到最大的gflops，程序得这样编写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
._cpufp.x86.sse.fp32.L1:
		mulps %xmm0, %xmm0
    addps %xmm1, %xmm1
    mulps %xmm2, %xmm2
    addps %xmm3, %xmm3
    mulps %xmm4, %xmm4
    addps %xmm5, %xmm5
    mulps %xmm6, %xmm6
    addps %xmm7, %xmm7
    sub $0x1, %rax
    mulps %xmm8, %xmm8
    addps %xmm9, %xmm9
    mulps %xmm10, %xmm10
    addps %xmm11, %xmm11
    mulps %xmm12, %xmm12
    addps %xmm13, %xmm13
    mulps %xmm14, %xmm14
    addps %xmm15, %xmm15

但是，这样显然意义不是很大，因为他要求乘数和被乘数是一个数，要真的合理的利用这些寄存器来做乘累加运算，需要编写8条指令，一共可以对16个double数来做操作，这样我们将原来的loop unroll展开到4*4，继续重复之前的步骤：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
for ( p=0; p<k; p++ ){
    a_0p_reg = A( 0, p );
    a_1p_reg = A( 1, p );
    a_2p_reg = A( 2, p );
    a_3p_reg = A( 3, p );

    b_p0_pntr = &B( p, 0 );
    b_p1_pntr = &B( p, 1 );
    b_p2_pntr = &B( p, 2 );
    b_p3_pntr = &B( p, 3 );

    /* First row */
    c_00_reg += a_0p_reg * *b_p0_pntr;
    c_01_reg += a_0p_reg * *b_p1_pntr;
    c_02_reg += a_0p_reg * *b_p2_pntr;
    c_03_reg += a_0p_reg * *b_p3_pntr;

    /* Second row */
    c_10_reg += a_1p_reg * *b_p0_pntr;
    c_11_reg += a_1p_reg * *b_p1_pntr;
    c_12_reg += a_1p_reg * *b_p2_pntr;
    c_13_reg += a_1p_reg * *b_p3_pntr;

    /* Third row */
    c_20_reg += a_2p_reg * *b_p0_pntr;
    c_21_reg += a_2p_reg * *b_p1_pntr;
    c_22_reg += a_2p_reg * *b_p2_pntr;
    c_23_reg += a_2p_reg * *b_p3_pntr;

    /* Four row */
    c_30_reg += a_3p_reg * *b_p0_pntr++;
    c_31_reg += a_3p_reg * *b_p1_pntr++;
    c_32_reg += a_3p_reg * *b_p2_pntr++;
    c_33_reg += a_3p_reg * *b_p3_pntr++;
}

这里，显然对于B来讲，也是可以用寄存器缓存的方式进行加速，但是，显而易见在这里我们使用的寄存器数量已经明显超过了我们可以使用的物理寄存器数量，但是这也不慌，因为用户不可见的重命名寄存器的数量还是够用的。

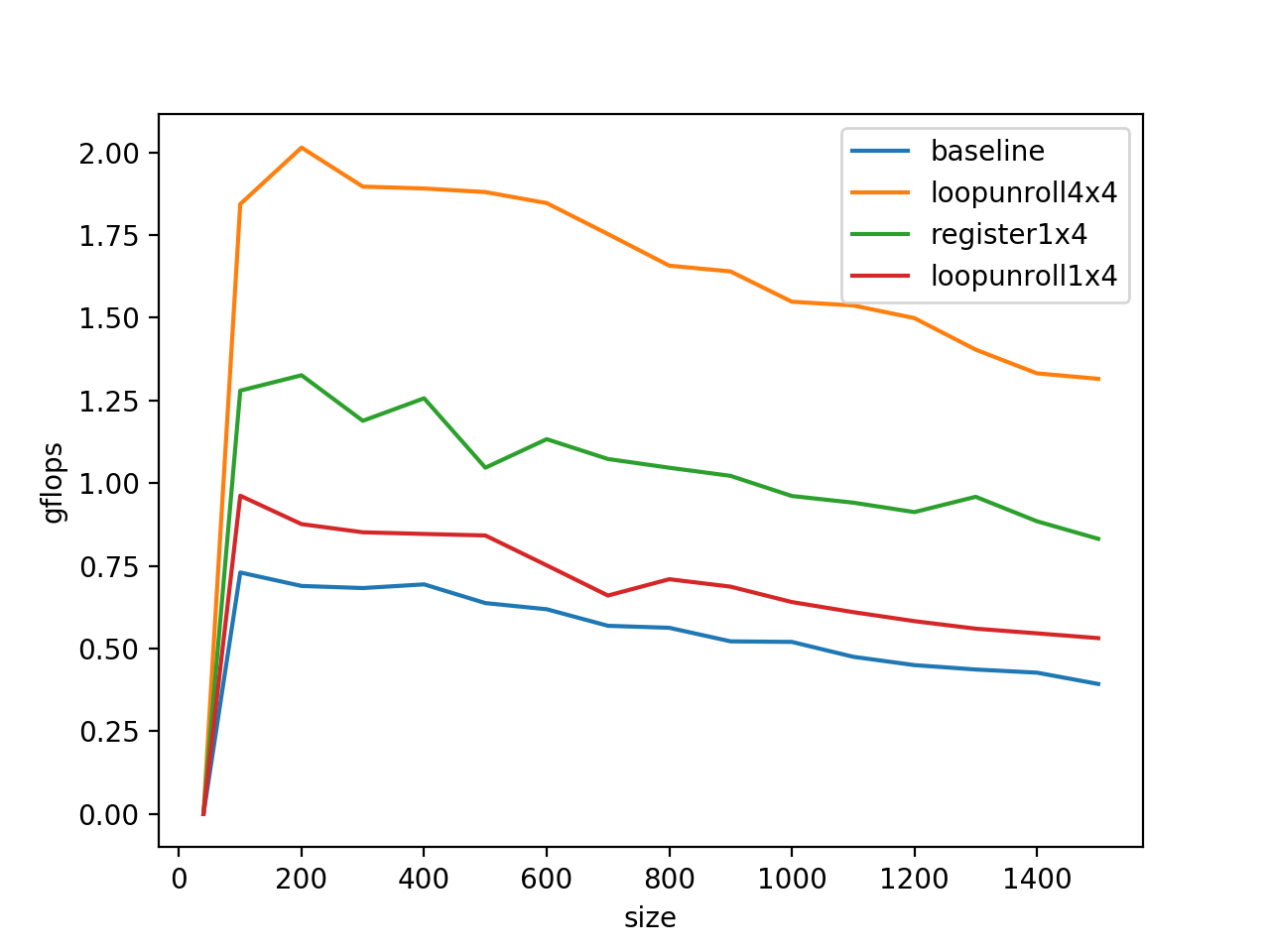
loopunroll4x4

对B做寄存器共用也带来了一定的performance，接下来我们尝试使用simd进行加速，选用的是SSE指令集。

关于X86的指令集，Intel提供了一套C API来调用，不需要我们手写汇编来实现。具体的做法是，将simd的操作数先塞到向量寄存器里去，接着直接使用乘法即可。

1
2
3
4
5
6
7
8
9
10
b_p0_vreg.v = _mm_loaddup_pd( (double *) b_p0_pntr++ );   /* load and duplicate */
b_p1_vreg.v = _mm_loaddup_pd( (double *) b_p1_pntr++ );   /* load and duplicate */
b_p2_vreg.v = _mm_loaddup_pd( (double *) b_p2_pntr++ );   /* load and duplicate */
b_p3_vreg.v = _mm_loaddup_pd( (double *) b_p3_pntr++ );   /* load and duplicate */

/* First row and second rows */
c_00_c_10_vreg.v += a_0p_a_1p_vreg.v * b_p0_vreg.v;
c_01_c_11_vreg.v += a_0p_a_1p_vreg.v * b_p1_vreg.v;
c_02_c_12_vreg.v += a_0p_a_1p_vreg.v * b_p2_vreg.v;
c_03_c_13_vreg.v += a_0p_a_1p_vreg.v * b_p3_vreg.v;

比如对于C_0_0、C_1_0 这两个数，有：
$$
C_{00} = \sum_{k=0}^{3}{A_{0k} * B_{k0}} \
C_{10} = \sum_{k=0}^{3}{A_{1k} * B_{k0}}
$$
分别把这两个表达式合并，一次做两个乘法，则A_0_k和A_1_k需要被塞到一起，使用_mm_load_pd指令，B_k_0两个运算都需要使用，需要在寄存器里复制一份，使用_mm_loaddup_pd指令。

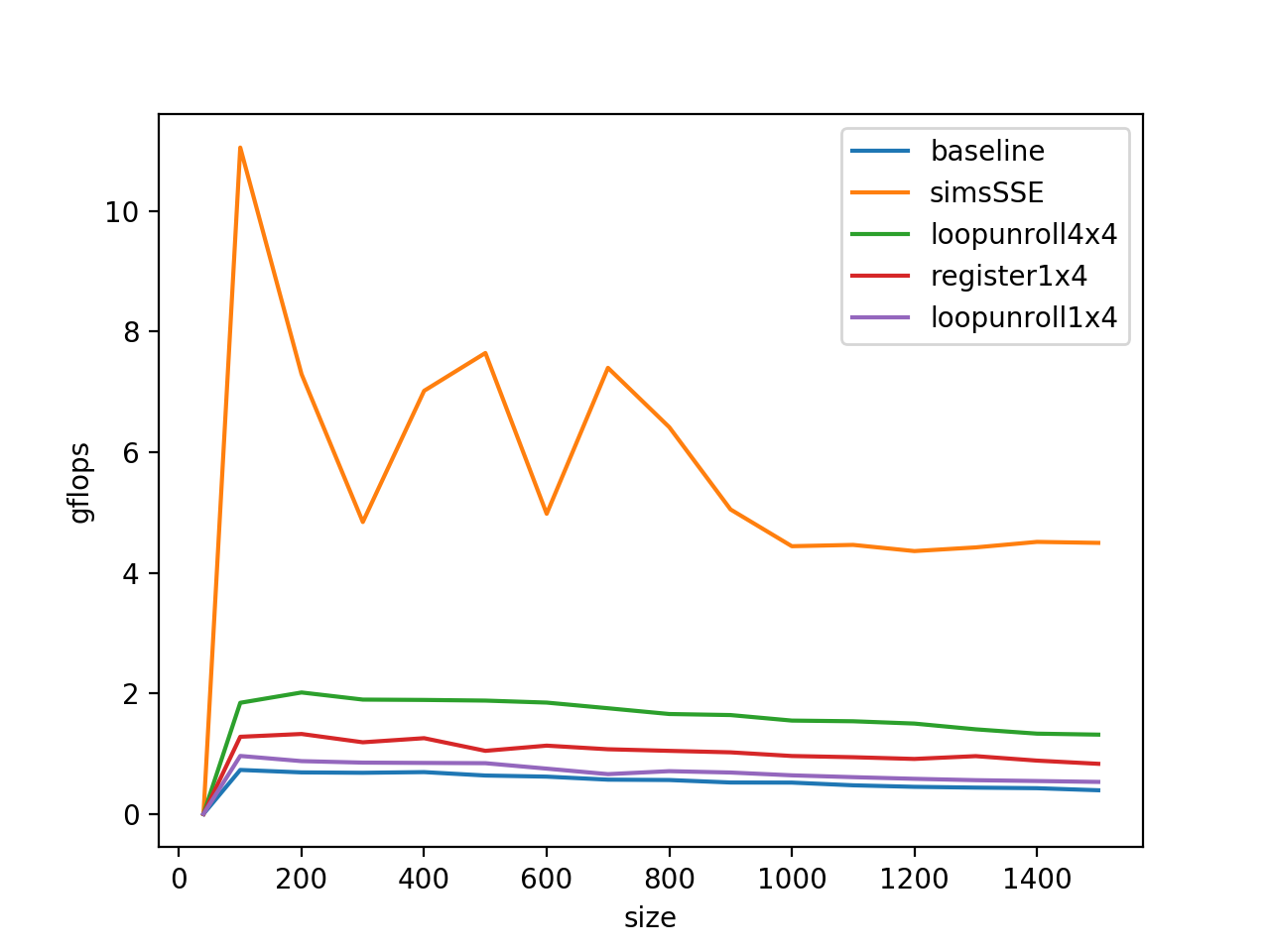
image-20220216162342131

在操作数的大小比较小的时候，程序已经基本上可以达到SSE指令集加速的最大gflops了（10 gflops）。

6. 矩阵分块乘法

不难注意到，使用了SIMD之后我们的程序的performance随着矩阵尺寸的扩大而降低的趋势变得更加严重，而造成这一现象的本质原因是矩阵过大的时候导致L2 Cache塞不下了，再次访问矩阵的头部元素就需要从DDR中交换数据，造成了访存瓶颈。

解决该问题的办法是矩阵分块，在著名的矩阵运算库GotoBLAS中是通过一个innerkernel来完成矩阵分块的，关于矩阵分块乘法的简单介绍参考这篇文章：https://zhuanlan.zhihu.com/p/133330692

根据Wik,Kaby Lake架构里，L2 Cache的大小是256Kb，在我们的程序里，将矩阵切分成最大256*128的小矩阵，由于小矩阵的元素是double，在我的机器上一个占8个字节，总大小为256*128*8=256KB。刚好可以填满 L2 Cache.

1
2
3
4
5
6
7
for ( p=0; p<k; p+=kc ){
    pb = min( k-p, kc );
    for ( i=0; i<m; i+=mc ){
        ib = min( m-i, mc );
        InnerKernel( ib, n, pb, &A( i,p ), lda, &B(p, 0 ), ldb, &C( i,0 ), ldc );
    }
}

这样再运行我们的程序：

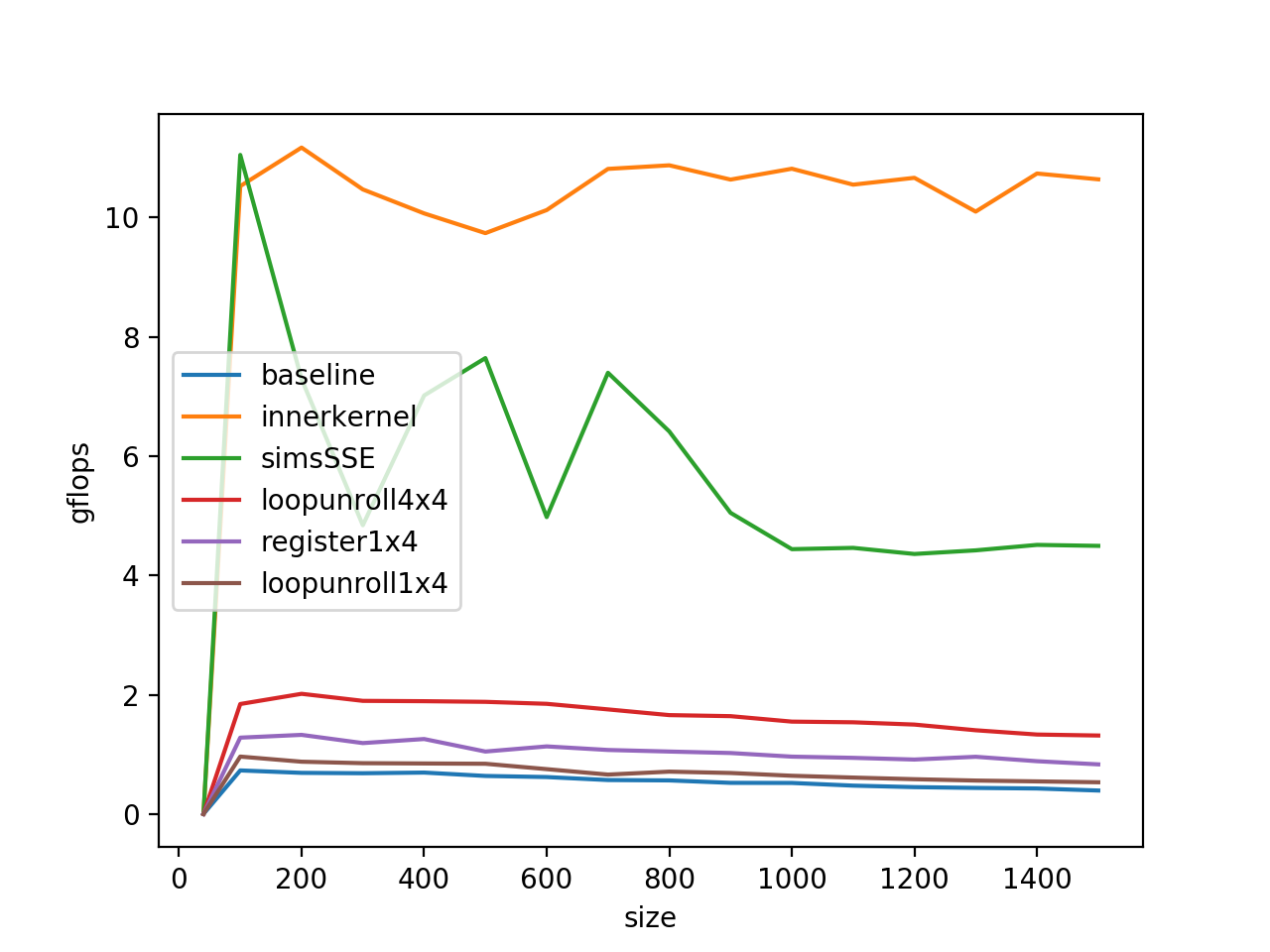
image-20220216165503348

随着尺寸上升性能下降的问题果然解决了！

7. DataPack

在how-to-optimize-gemm这里，最后还做了一个data pack来做性能的进一步提升（其实这一步主要是解决了我们程序设计的缺陷，不是gemm本身速度慢的问题，因为为了能够测到各个尺寸的benchmark，我们是直接开辟了一个1500*1500的大数组，再基于这个大数组做的运算，所以在访存的时候跨度会比较大，解决的办法就是开辟一个临时的小数组进行运算，最后程序得到性能如下图：

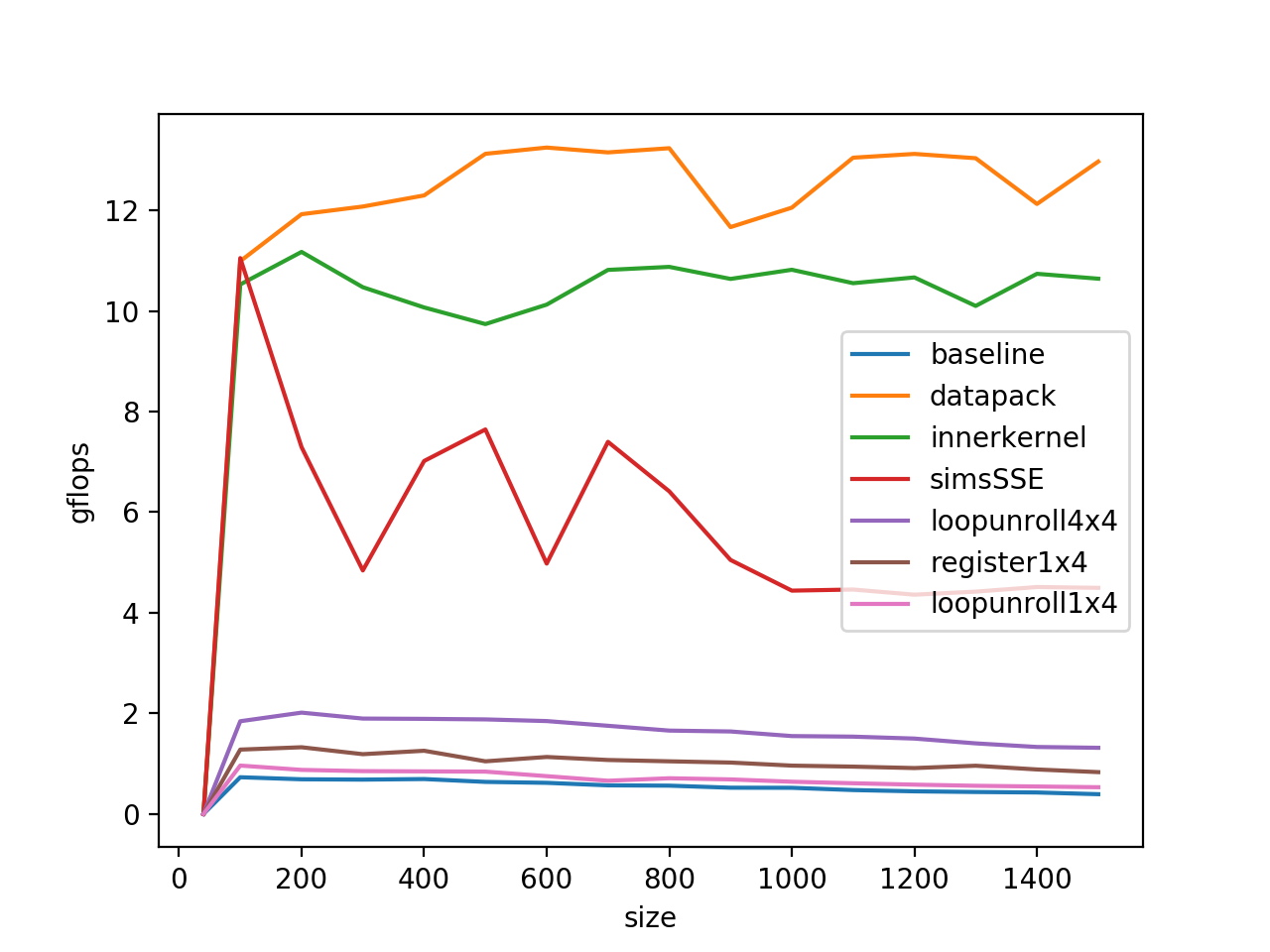
image-20220216170201568

#Compiler #Optimization
论文阅读｜Dual-side Sparse Tensor Core CMake Notes

Comments

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×