AI Computing System

Technical 33 minutes read (About 4884 words)

banner

Github Page: https://github.com/LeiWang1999/AICS-Course

第一章 概述

1.1 简述强人工智能和弱人工智能的区别

人工智能大致分为两大类：强人工智能和弱人工智能。弱人工智能(weak artificial intelligence)是能够完成某种特定具体任务的人工智能，换个角度看，就是一种计算机科学非常平凡的应用。强人工智能(strong artificial intelligence)或通用人工智能，是具备与人类同等智慧，或超越人类的人工智能，能表现正常人类所具有的所有智能行为。（摘录自课本 Page 1）

1.2 简述人工智能研究的三个学派

人工智能按研究学派主要分为三类，包括行为主义(Behaviorism)，符号主义(Symbolism)，连接主义(Connectionism)。（摘录自课本 Page 2）

行为主义的核心思想是基于控制论构建感知-动作型控制系统。（摘录自课本 Page 2） 在 C.Shannon 和 J.McCarthy 征集出版的《自动机研究》中有很多控制论方面的研究工作，涉及有有限自动机，图灵机、合成自动机，希望基于控制论去构建一些感知动作的反应性的控制系统。从比较直观的角度来看，行为主义的方法可以模拟出类似于小脑这样的人工智能，通过反馈来实现机器人的行走、抓取、平衡，因此有很大的实用价值。但是，这类方法似乎并不是通向人工智能的终极道路。（摘录自课本 Page 5）

符号主义是基于符号逻辑的方法，用逻辑表示知识和求解问题。其基本思想是：用一种逻辑把各种知识都表示出来；当求解一个问题时，就将该问题转化成一个逻辑表达式，然后用已有知识的逻辑表达式的库进行推理来解决该问题。但从逻辑的角度，难以找到一种简洁的符号逻辑体系，能表述出世间所有的知识。（摘录自课本 Page 5） 从常识的角度，研究者还没能把一个实用领域中的所有常识都用逻辑表达式记录下来。从求解器的角度来看，解决问题的关键环节是逻辑求解器，而各种谓词逻辑一般都是不可判定的，也就是理论上不存在一种机械方法，能在有限时间内判定任意一个谓词逻辑表达式是否成立。（摘录自课本 Page 6）

连接主义方法的基本出发点是借鉴大脑中神经元细胞连接的计算模型，用人工神经网络来拟合智能行为。（摘录自课本 Page 6） 连接主义方法始于 1943 年，从最开始的 M-P 神经元模型，到感知器模型、反向传播训练方法、卷积神经网络、深度学习、深度学习和反向传播训练方法，连接主义逐渐成为整个人工智能领域的主流方向。但是我们必须清楚的认识到，深度学习不一定是通向强人工智能的终极道路。它更像是一个能帮助我们快速爬到二楼、三楼的梯子，但顺着梯子我们很难爬到月球上。深度学习已知的局限性包括：泛化能力有限、缺乏推理能力、缺乏可解释性、鲁棒性欠佳等。（摘录自课本 Page 7 Page 8）

1.3 一个由两个输入的单个神经元构成的感知机能完成什么任务？

首先，感知器是只有输入和输出层的神经网络:

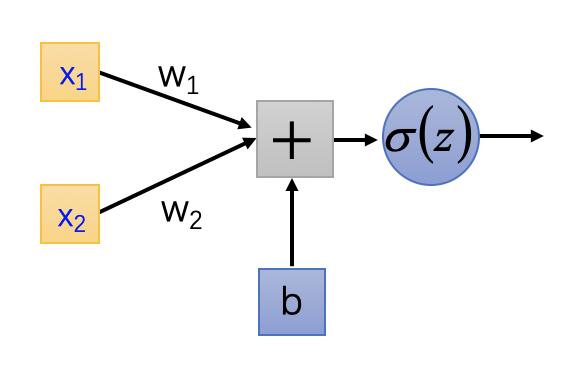
sensor

在 1958 年，由美国心理学家 Frank Rosenblatt 提出的感知器模型中，激活函数采用的一般是符号函数，及输出

$$o = sgn(x_1w_1+x_2*w_2+b)$$

进一步表示为：

$$\begin{cases} 1, & x_1w_1+x_2 * w_2+b>=0 \\ -1, & x_1w_1+x_2*w_2+b<0 \end{cases}$$

如果把$o$当作因变量、$x_1、x_2$当作自变量，对于分界

$$x_1w_1+x_2w_2+b=0$$

可以抽象成三维空间里的一个分割面，能够对该面上下方的点进行分类，则及该感知机能完成的任务是用简单的线性分类任务，比如可以完成逻辑“与”与逻辑“或”的分类(在这里，第三维度只有 1 和-1 两个值，分别使用实心点和空心点来表征，这样就可以在二维平面上将问题可视化)：

  1. 逻辑“与”的真值表和二维样本：

    $x_1$ $x_2$ $x_3$
    0 0 0
    0 1 0
    1 0 0
    1 1 1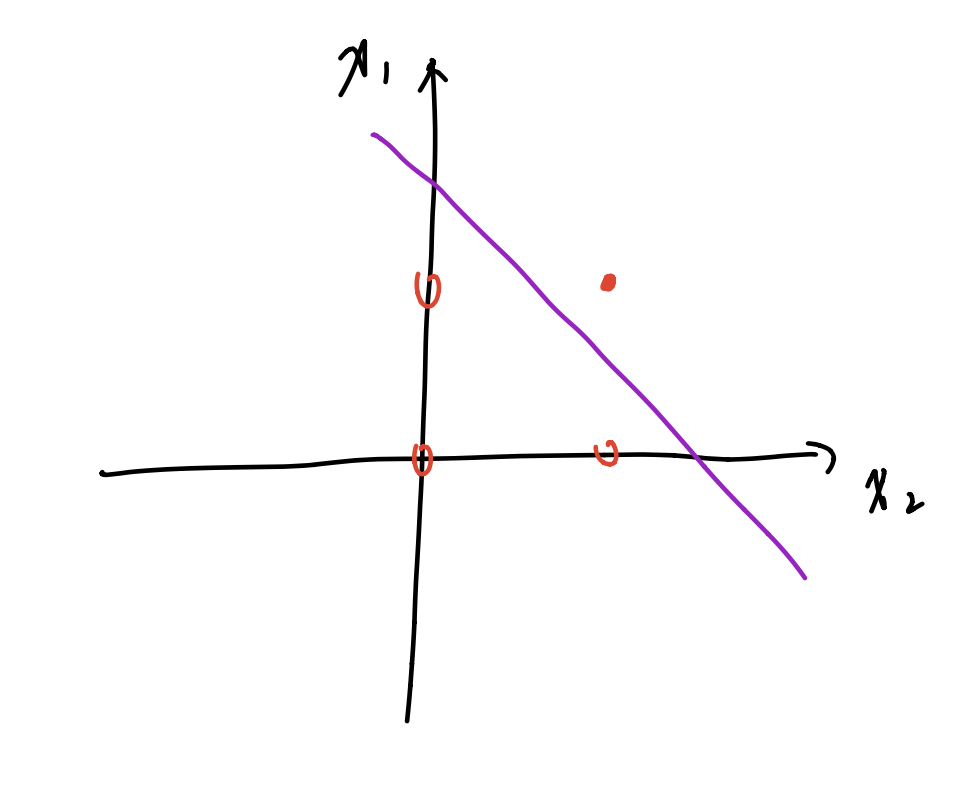
    与逻辑

  2. 逻辑“或”的真值表和二维样本:

    $x_1$ $x_2$ $x_3$
    0 0 0
    0 1 1
    1 0 1
    1 1 1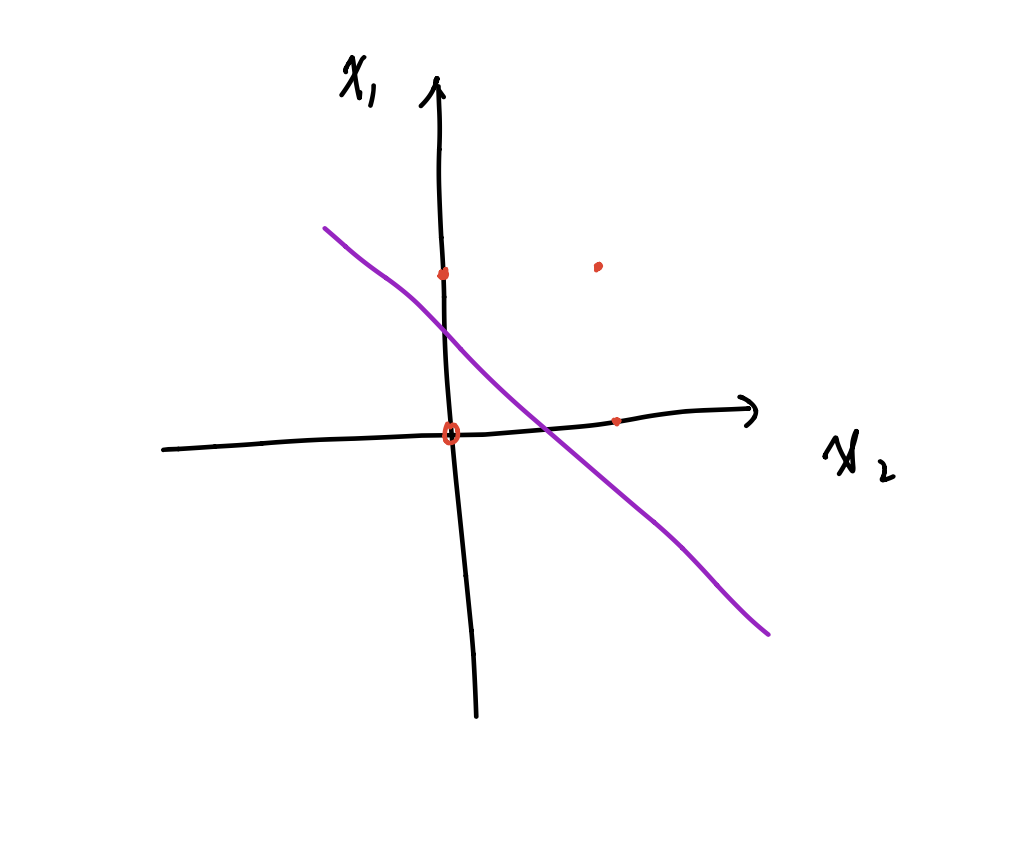
    逻辑或

但是对于非线性问题，如异或问题，单层感知机就没办法实现了：

$x_1$ $x_2$ $x_3$
0 0 0
0 1 1
1 0 1
1 1 0
逻辑异或

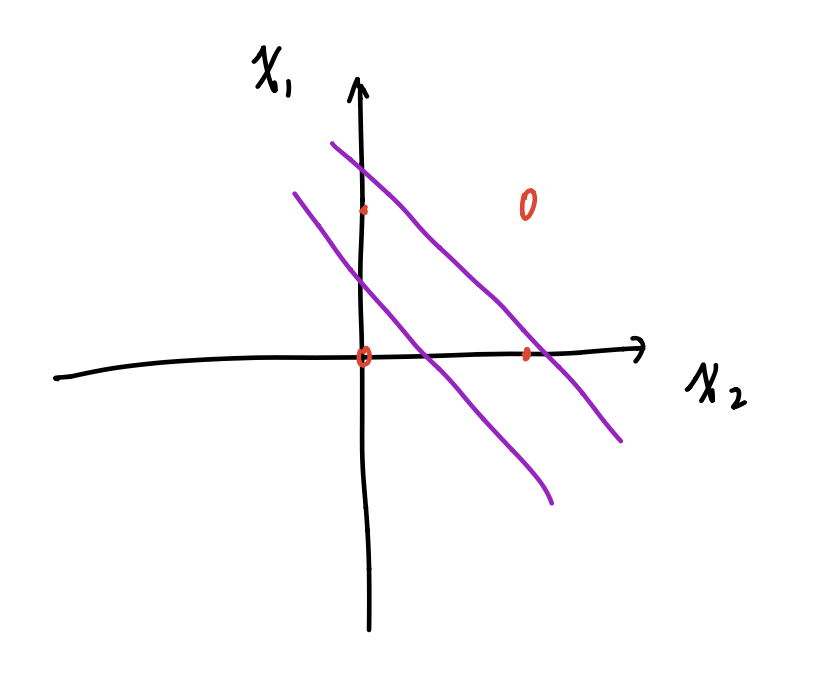
多层感知机能够实现这一点，这篇博客指出了这样一个观点:Kolmogorov 理论指出： 双隐层感知器就足以解决任何复杂的分类问题.但我没有找到相关的证明，就和 8bit 就足够表示 Feature Map 一样迷惑，在这篇文献：

  • [1].APPROXIMATION CAPABILITIES OF MULTILAYER FEEDFORWARD REGULAR FUZZY NEURAL NETWORKS[J].Applied Mathematics:A Journal of Chinese Universities,2001(01):45-57.

K.Hornik 证明了理论上只有一个隐层的浅层神经网络足以拟合出任意函数。但有个假设前提：一个隐层的深度可以是无限，这样就好理解了。

我找到了一篇相对清晰的证明，感兴趣的同学可以看看：https://www.cnblogs.com/yeluzi/p/7491619.html

1.4 深度学习的局限性有哪些？

深度学习已知的局限性包括：

(1)泛化能力有限。 深度学习训练需要依靠大量的样本，与人类学习的机理不同。人类在幼儿时期会依据大量外在数据学习，但是成年人类的迁移学习能力和泛化能力远高于现在的深度学习。

(2)缺乏推理能力。 缺乏推理能力使得深度学习不擅长解决认知类的问题。如何将擅长推理的符号逻辑与深度学习结合起来，是未来非常有潜力的发展方向。

(3)缺乏可解释性。 在比较重视安全的领域，缺乏可解释性会带来一些问题。比如，某个决策是如何做出来的？深度学习为什么识别错了。

(4)鲁棒性欠佳。 在一张图像上加一些人眼很难注意到的点，就可以让深度学习算法产生错误判断，例如把猪识别成猫，把牛识别成狗。

（摘录自课本 Page 7 Page 8）

1.5 什么是智能计算系统？

智能计算系统是智能的物质载体。（摘录自课本 Page 8）

1.6 为什么需要智能计算系统？

传统计算系统的能效难以满足应用需求。因此，人工智能不可能依赖于传统计算系统，必须有自己的核心物质载体–智能计算系统。（摘录自课本 Page 8）

1.7 第一代智能计算系统有什么特点？

第一代智能计算系统主要是在 20 世纪 80 年代人工智能发展的第二次热潮中发展起来的面向符号逻辑处理的计算系统。它们的功能主要是运行当时非常热门的智能编程语言 Prolog 或 LISP 编写的程序。（摘录自课本 Page 9）

1.8 第二代智能计算系统有什么特点？

第二代智能计算系统主要研究面向连接主义（深度学习）处理的计算机或处理器。（摘录自课本 Page 10）

1.9 第三代智能计算系统有什么特点？

编者团队认为，第三代智能计算系统将不再单纯追求智能算法的加速，它将通过近乎无限的计算能力，给人类带来前所未有的机器智能。（摘录自课本 Page 11）

1.10 假如请你设计一个智能计算系统，你打算如何设计？在你的设计里，用户将如何使用该智能计算系统？

假如让我设计一个第二代的智能计算系统，我的方案如下：

硬件层面，借助VTA的设计思想，设计 Load、Compute、Store 三个模块，Load 负责从 DDR 中缓存数据，Store 负责将运算结果放回到 DDR，在 Compute 模块里，设计一些大运算需要的加速器，例如使用脉动阵列(Systolic Array)加速矩阵乘法、快速卷机(Fast Convolution)做卷积运算等等。

软件层面:

  1. 需要设计一套 AI 指令集，告诉加速器缓存/放回的数据地址，以及对相应数据做的 Compute 操作。
  2. 软件上层对所需的运算，例如接受一个通用的神经网络模型，做硬件无关的优化，比如神经网络压缩，图优化，算子融合等。
  3. 此外，在上层还需要做出合适的任务调度，把计算不复杂，控制性较强的部分交给 CPU 处理，把适合加速器运算的交给加速器运算，组成一个异构系统。
  4. 软件还需要提供用户接口，可以是 Python/C++等主流编程语言。

用户使用该智能计算系统时，在 Python 中编写相关的程序，调用配套编程框架做上层软件优化，以及对任务的调度安排，生成可以在我设计的智能计算系统上的可执行文件，用户执行该可执行文件，并给可执行文件一个输入，产生经过系统加速后的输出。

但是该系统的缺点也很明显，从底层硬件到上层软件栈，战线拉的太长了，而且硬件层面流片的成本巨大，但是深度学习所需的算子繁多并且在茁壮成长，硬件应当也需要不断的迭代更新。所以可以考虑把硬件加速的这部分换成 FPGA 来实现，如果需要新增算子或者更改，重新综合生成相关电路即可。

第二章、神经网络基础

2.1 多层感知机和感知机的区别是什么，为什么会有这样的区别？

感知机是只有一个神经元的单层神经网络。（摘录自课本 Page 17）

多层感知机是 20 世纪八九十年代常用的一种两层的神经网络。（摘录自课本 Page 19）

首先，感知机和多层感知机都可以接受若干个输入，但感知机只能有一个输出，多层感知机可以有多个输出。

此外，相比感知机而言，多层感知机可以解决输入非线性可分的问题。

2.2 假设有一个只有一个隐层的多层感知机，其输入、隐层、输出层的神经元个数分别为 33、512、10，那么这个多层感知机中总共有多少个参数是可以被训练的？

确定 weight 的个数：

$$
weights = 33 * 512 +512*10= 22016
$$

确定 bias 的个数：

$$
biases =1+1=2
$$

这样，总共可以被训练的参数是 22018 个。

2.3 反向传播中，神经元的梯度是如何计算的？权重是如何更新的？

基于梯度下降法的神经网络反向传播过程首先需要根据应用场景定义合适损失函数（loss function），常用的损失函数有均方差损失函数和交叉熵损失函数。确定了损失函数之后，把网络的实际输出与期盼输出结合损失函数计算 loss，如果 loss 不符合预期，则对 loss 分别求权重和偏置的偏导数，然后沿梯度下降方向更新权重及偏置参数。

不引入惩罚项的权重更新公式如下：

$$
w \gets w-\eta(\triangledown_wL(w;x,y))
$$

2.4 请在同一个坐标系内画出五种不同的激活函数图像，并比较它们的取值范围。

仓库地址：https://github.com/LeiWang1999/AICS-Course/blob/master/Code/2.4.activationplot.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1.0/(1.0+np.exp(-1.0 * x))

def tanh(x):
    return (np.exp(x)-np.exp(-1.0 * x))/(np.exp(x)+np.exp(-1.0 * x))

def ReLU(x):
    return np.maximum(0, x)

def PReLU(x, a=-0.01):
    return np.maximum(a*x, x)

def ELU(x, a=-0.01):
    y = np.zeros_like(x)
    for index, each in enumerate(x):
        y[index] = each if each>0 else a*(np.exp(each)-1.0)
    return y

x=np.linspace(-10,10,256,endpoint=True)#-π to+π的256个值
y_sigmoid = sigmoid(x)
y_tanh = tanh(x)
y_ReLU = ReLU(x)
y_PReLU = PReLU(x)
y_ELU = ELU(x)
plt.grid() # 生成网格
plt.plot(x, y_sigmoid, label='sigmoid')
plt.plot(x, y_tanh, label='tanh')
plt.plot(x, y_ReLU, label='ReLU')
plt.plot(x, y_PReLU, label='PReLU')
plt.plot(x, y_ELU, label='ELU')
plt.legend(['sigmoid','tanh', 'ReLU', 'PReLU', 'ELU'])
plt.show()

绘图结果如下：

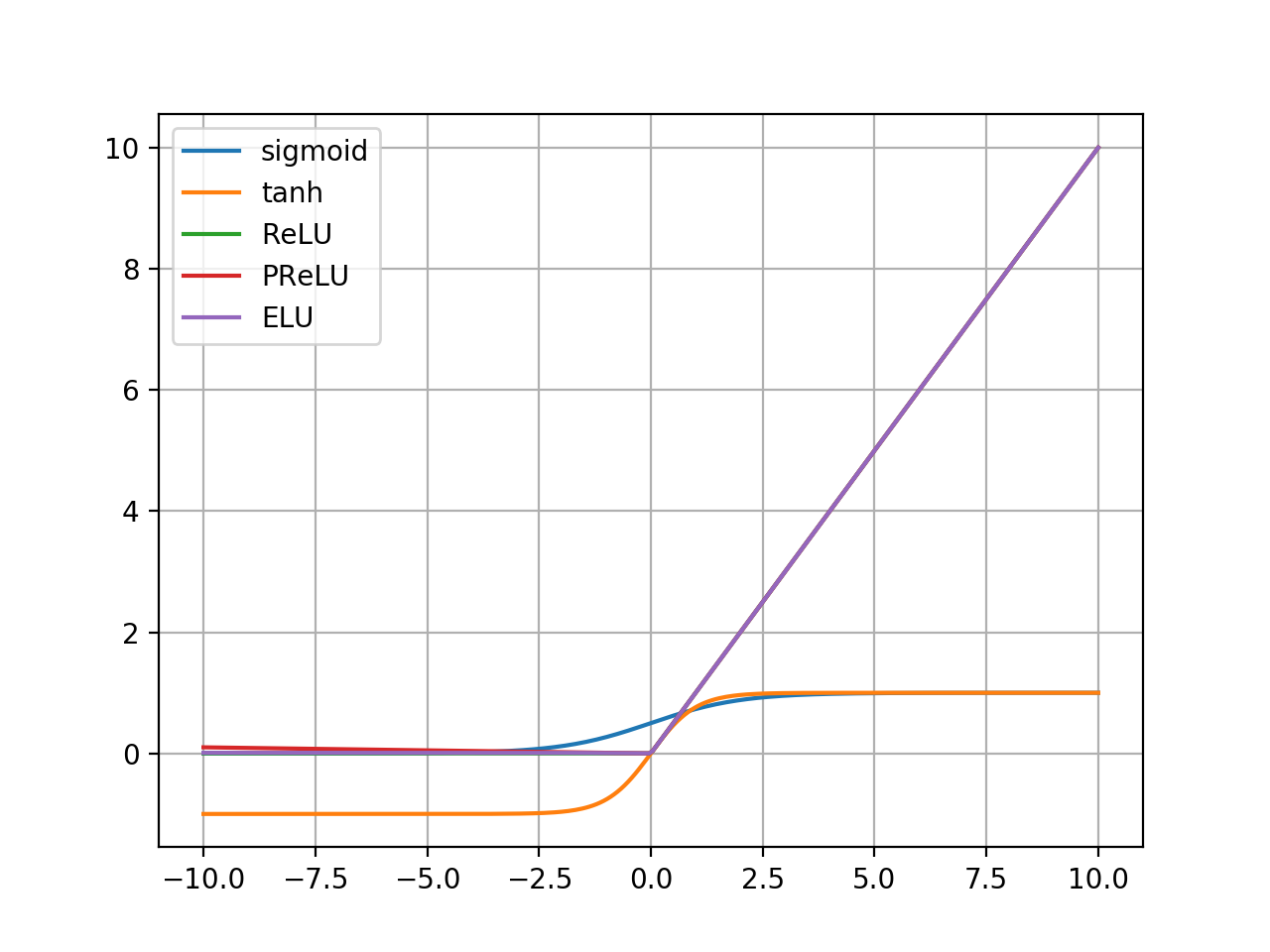
Figure_1

对输入取区间[-10, 10],a 取-0.01:比较取值范围：

Function Minimum Maximum
sigmoid 0 1
tanh -1 1
ReLU 0 10
PReLU -0.1 10
ELU 0.00038 10

2.5 请简述三种避免过拟合问题的方法

  1. 在损失函数中增加惩罚项，常用的方法有 L1 正则化和 L2 正则化，L1 正则化可以使训练出来的 weight 更接近于 0，L2 正则化可以使全中国 weight 的绝对值变小。
  2. 稀疏化，在训练的时候将神经网络中的很多权重或神经元设置成 0，也是通过增加一些惩罚项来实现的。
  3. Bagging 集成学习，应对一个问题时训练几个不同的网络，最后取结果的加权，减少神经网络的识别误差
  4. Dropout 会在训练的时候随机删除一些节点，往往会起到意想不到的结果，一般来说我们设置输入节点的采样率为 0.8，隐层节点的采样率为 0.5。在推理阶段，我们再将对应的节点输出乘以采样率，即训练的时候使用 Dropout，但是推理的时候会使用未经裁剪的整个网络。

2.6 sigmoid 激活函数的极限是 0 和 1，请给出它的导数形式并求出其在原点的值

sigmoid 函数如下：

$$
sigmoid(x) = \frac{1}{1+e^{-x}}
$$

求 sigmoid 函数的导数:

$$
\frac{\mathrm{d}sigmoid(x)}{x} = \frac{e^{-x}}{(1+e^{-x})^2}=\frac{1}{e^{-x}+e^x+2}
$$

在原点处的值为:

$$
\frac{1}{1+1+2}=0.25
$$

2.7 假设激活函数的表达式为$\phi(v)=\frac{v}{\sqrt{1+v^2}}$，请给出它的导数形式并求出其在原点的取值

$$
\frac{\mathrm{d}\phi(v)}{\mathrm{d}v}=\frac{\mathrm{d}v*(1+v^2)^{-1/2}}{\mathrm{d}v}=\frac{\mathrm{d}(1+v^2)(1+v^2)^{-3/2}+\mathrm{d}-v^2(1+v^2)^{-3/2}}{\mathrm{d}v}=\frac{1}{(1+v^2)^{3/2}}
$$

当在原点处时，该激活函数的导数取值为 1。

2.8 假设基本采用表 2.1 中的符号，一个经过训练的有两个隐层的 MLP 如何决定各个输出神经元的标签？预测过程中，当前输入的样本的标签如何决定？

题目没有给出，两个隐藏层的神经元个数是多少个，我们可以假设输入矩阵为x，输入层和第一层隐层的权重为w1，第一层隐层和第二层隐层的权重为w2.输出为y，则有:

$$
temp=w_1^Tx \\
y = w_2^Ttemp
$$

输出样本的标签由输出y的最大值的下标决定。

2.9 一种更新权重的方法是引入动量项，公式如下，动量 a 的取值范围通常为[0, 1]，这样对于权重更新有什么影响？如果取值范围是[-1,0]呢？

$$
\triangle w(n) = a\triangle w(n-1)+a^2\triangle w(n-2)+…
$$

当 a 为[0,1]时，动量项表现为惩罚项，每一次求梯度的时候都会考虑到之前几步更新权重的的动量，并且距离越近影响越大，梯度更新的曲线会越平滑，并且因为考虑到动量，就有可能突破 local minimal，找到 global minimal。具体的知识可以以momentum为 keyword 搜索相关资料。

当 a 为[-1,0]时，动量项表现为奖励项，这样梯度的收敛曲线应该会更陡峭，至于有啥用途想不到。

2.10 反向传播中，采用不同的激活函数对于梯度的计算有什么不同？请设计一个新的激活函数并给出神经元的梯度计算公式。

梯度的计算需要求目标函数关于权重和偏置的偏导数，激活函数不同会导致偏导数不同，进而影响梯度的计算。

设计一个新的激活函数：

$$
\delta(z) = e^z
$$

对一个简单的神经元：

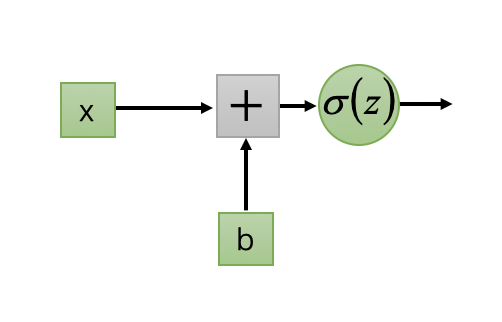
sensor

则有

$$
y = \delta(wx+b)=e^{wx+b}
$$

选择目标函数为均方误差（mean-square error, MSE）：

$$
Loss=(\check y - y)^2 = (\check y - e^{w*x+b})^2
$$

神经元的梯度计算公式:

$$
\triangledown_w=\frac{\partial Loss}{\partial w}=-2xe^{wx+b}(\check y - e^{wx+b}) \\
\triangledown_b=\frac{\partial Loss}{\partial b}=2e^{wx+b}(\check y - e^{wx+b})
$$

2.11 请设计一个多层感知机实现 4 位全加器的功能，即两个 4 比特输入得到一个 4 比特输出以及 1 比特进位。请自行构建训练集、测试集，完成训练及测试。

Github Code Link：https://github.com/LeiWang1999/AICS-Course/tree/master/Code/2.11.fulladder.pytorch

框架：Pytorch

网络结构：简单的 MLP、两个隐层 layer、各 20 个 node、激活函数使用的是 Relu。

1
2
3
4
5
6
7
8
9
10
11
12
class MLP(nn.Module):
    def __init__(self, input_dim, hidden_1, hidden_2, output_dim):
        super(MLP,self).__init__()
        self.layer1 = nn.Sequential(nn.Linear(input_dim, hidden_1), nn.ReLU(True))
        self.layer2 = nn.Sequential(nn.Linear(hidden_1, hidden_2), nn.ReLU(True))
        self.layer3 = nn.Sequential(nn.Linear(hidden_2, output_dim))

    def forward(self,x):
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        return x

数据集构建：

  1. 使用 python 实现二进制全加器(binary_adder.py)、然后遍历输出构建数据集
  2. 对数据集做了 shuffle，再分出训练集和测试集、这样提取的特征更准确

200 个 epoch 可以达到 100%的准确率：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[epoch 194] train_loss: 0.920  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0021
 time.perf_counter()-t1
[epoch 195] train_loss: 0.929  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0021
 time.perf_counter()-t1
[epoch 196] train_loss: 0.979  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0021
 time.perf_counter()-t1
[epoch 197] train_loss: 1.004  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0020
 time.perf_counter()-t1
[epoch 198] train_loss: 0.995  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0020
 time.perf_counter()-t1
[epoch 199] train_loss: 0.927  test_accuracy: 1.000
train loss: 100%[*************************************************->]0.0010
 time.perf_counter()-t1
[epoch 200] train_loss: 0.979  test_accuracy: 1.000
Finished Training

2.12 在不使用编程框架的前提下，重新实现解决习题 2.11 的代码。

Github Code Link:https://github.com/LeiWang1999/AICS-Course/tree/master/Code/2.12.fulladder.cpp

#AICS
2020.12 What i Read 2020.11 What i Read

Comments

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×