编译高级教程｜学习笔记

这篇文章是2021年中国科学院大学李炼老师的《编译程序高级教程》一课的学习笔记，这门课程的内容主要是基于LLVM来做一些中间代码的优化。不建议没有学习或者了解过编译原理的同学选修，平时作业占比较大，一共三次大作业共占期末总成绩的80分，然后是期末考试只有20分（而且可以使用离线的电子设备。但是作业爆炸难，是使用LLVM来实现一些程序分析，实现一个简单的C程序解释器、数据流分析、指针分析等。很多知识也是在我写这篇笔记的整理与复习的过程中才看明白的。

相似的课程为多伦多大学的CSCD70。而且就在考试的前一周，国内也有这方面可以看的公开课视频了，那就是南京大学的软件分析，兄弟们把泪目打在公屏上！

还有一些非常有用的参考资料：

• BUAA miniSysY Tutorial
• LLVM Lang Ref
• LLVM Programmer Manual
• LLVM Clang Study Notes
• PLCT bilibili chainnel

基本知识

基本块（Basic Block）

基本块是具有原子属性的指令集合，原子属性的含义就是如果基本块中的某一段代码被执行了，那么基本块中的代码肯定全部都会被执行。构建基本块的方法是：

1. 确定基本块的入口入口语句:
   • 程序的第一个语句
   • 能由条件转移语句和无条件转移语句转移到的语句，值得注意的是call 指令也是非分支指令，因为我们只关心call返回的结果。
   • 紧跟在条件/无条件转移语句后面的语句
2. 根据入口语句就可以构造出基本块：由该入口语句到下一个入口语句(不包括该入口 语句)、或到一转移语句之间的语句序列组成。凡未被纳入某一基本块中的语句，是程序中控制无法达到的语句，删除这个语句。

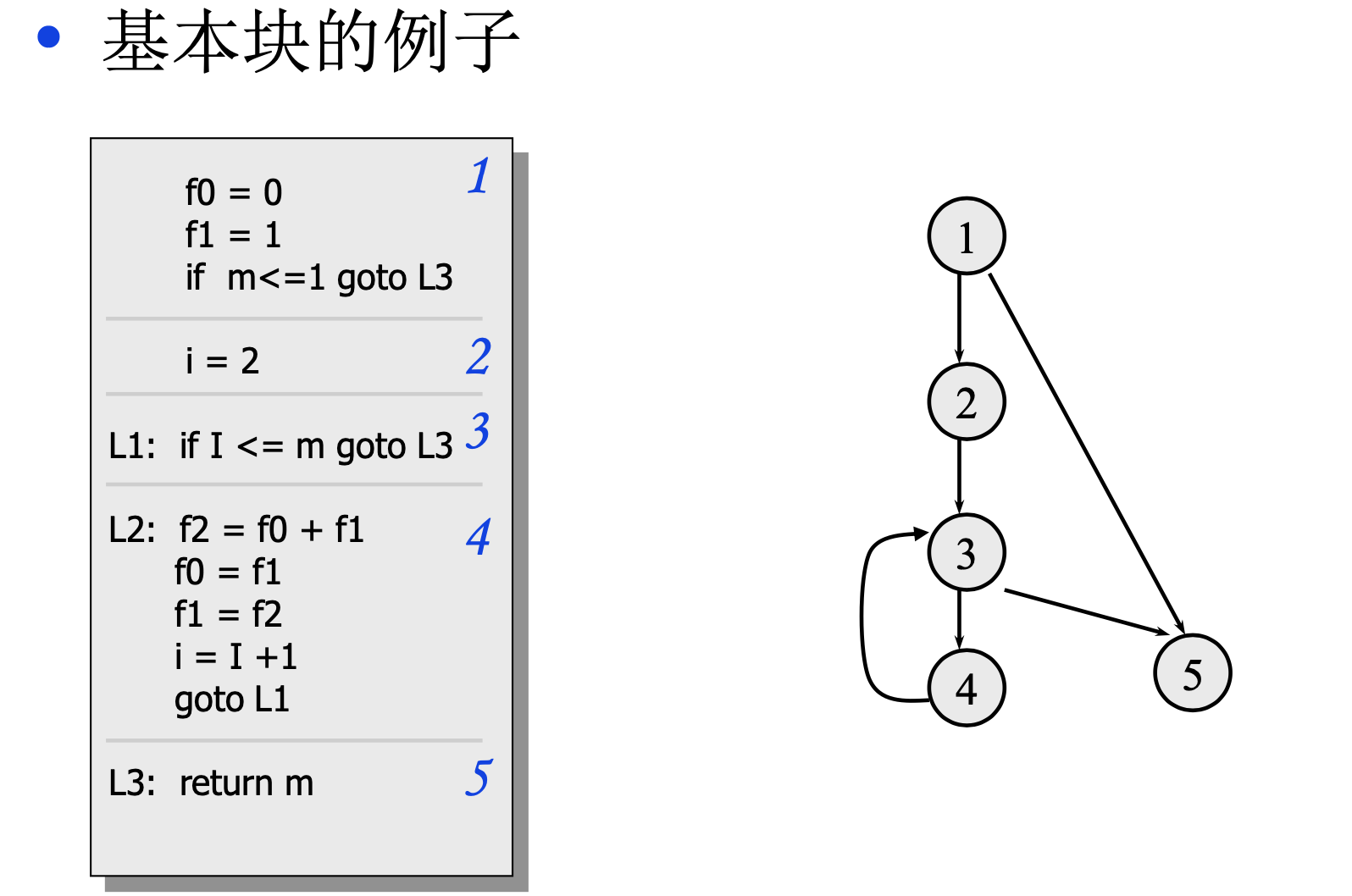
基本块也可以使用有向无环图的方式进行表示基本块内的计算过程，例如：

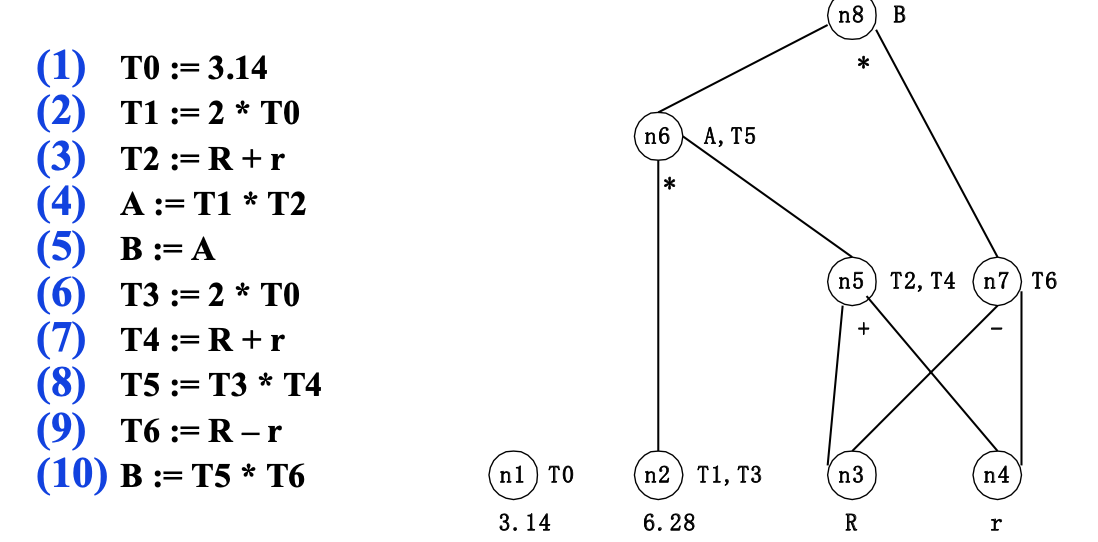
其中：

• 叶结点表示标识符或常数
• 内部结点表示运算
• 边表示了操作间的前驱和后继的关系

构造DAG可以做到：合并已知量，如T1，T3；删除冗余赋值，如B的第一次赋值；公共子表达式的提取，如T2和T4，在基本块外被定值并在基本块内被引用的所有标识符，就是作为叶结点上标记的那些标识符在基本块内被定值且该值能在基本块后面被引用的所有标识符，就是DAG各结点上的那些附加标识符。

但是这种基本块内部的数据流分析方法属于Local Analysis，做到的优化有限，LLVM/Clang里使用的是基于全局的，利用多个基本块信息构建的数据流分析。

控制流图（Control Flow Graphs）

控制流图是很多程序分析 和全局优化技术的基础，控制流图的节点是一些基本块。在基本块举的例子里，右侧的图片就是一个控制流图，关于根据控制流图求出控制节点、得到控制树、求基本块的控制边界是比较难的，我会放到构造SSA这一讲来解释，因为在构造SSA时需要插入phi节点，插入phi节点需要得到基本块的控制边界信息，为了得到控制边界信息需要先求出控制树，为了构造控制树，需要求出基本块的控制节点。

这里，主要讲下控制流图中的循环与回边两个概念。

怎样才是循环？

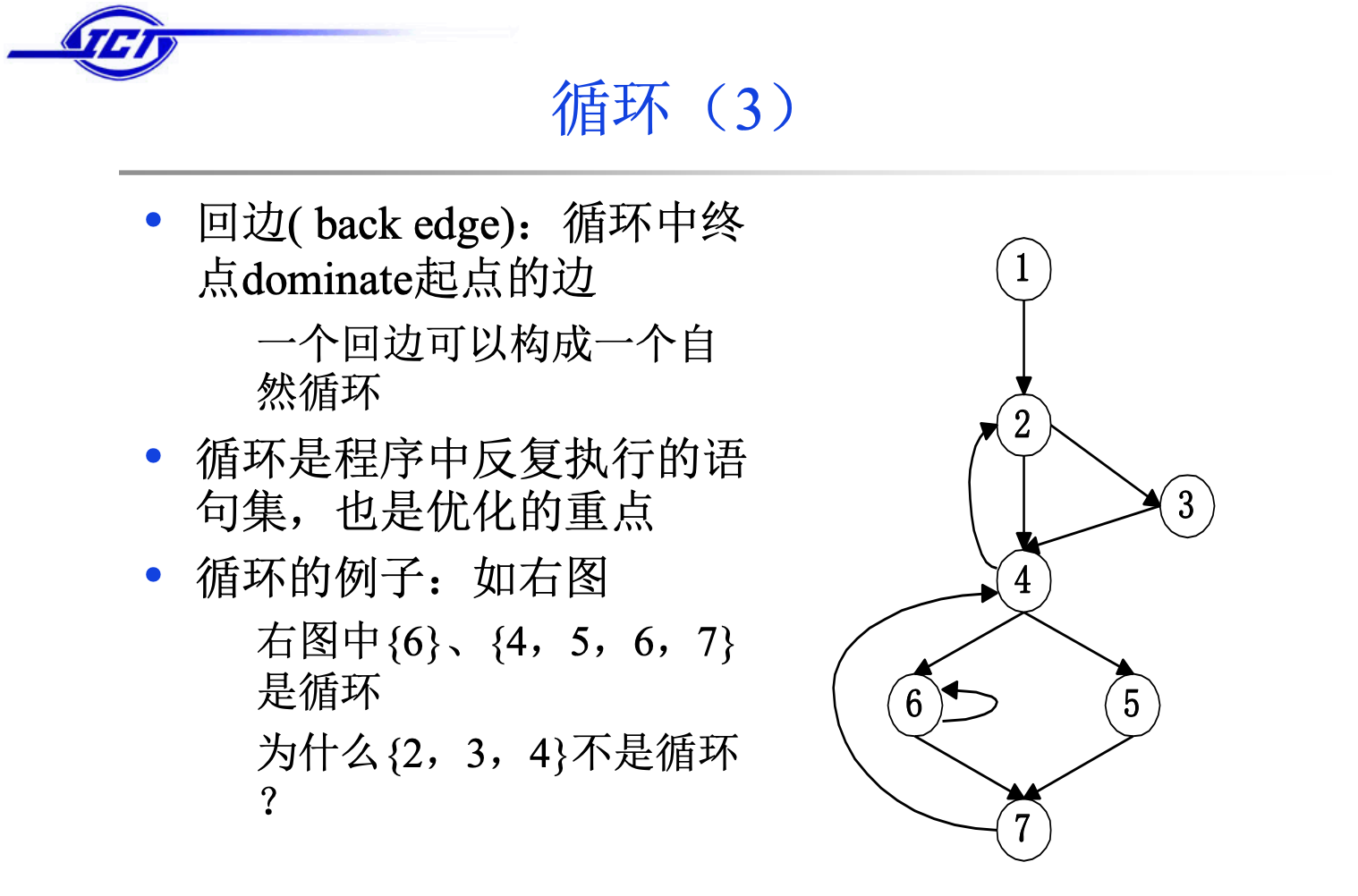
关于为什么{6}、{4, 5, 6, 7}是循环，这个大家都能感受出来，可是为什么{2, 3, 4}不是一个循环呢？因为在这个cycle里节点2和节点4都是entry point，所以他们不是循环。仔细想一下，一个循环肯定只有一个进入的节点，我们不可能突然跳到循环内部去执行某段代码。

intuitive properties of a loop：

• 只有一个entry point
• 边至少有一个循环

循环是程序中反复执行的语句，也是优化的重点。寻找循环的算法：

算法运行的结果：

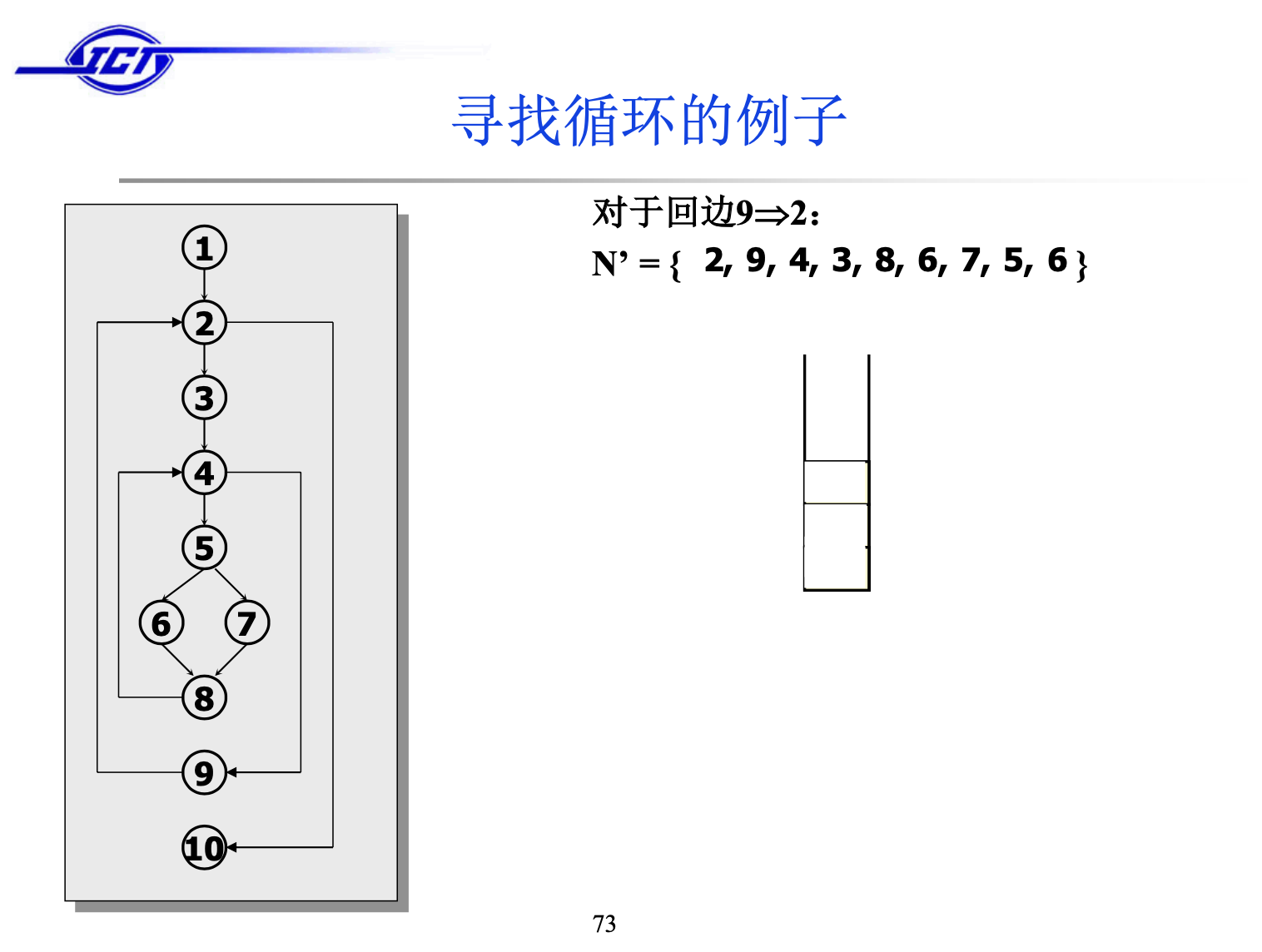
N’表示的是Loops数组，自己模拟运行一下代码，与结果是一致的。

回边(back edge)是循环中终点dominate起点的边，一条回边至少是一个循环的一部分。一条回边可以构成一个自然循环(natural loop)，自然循环是我们进行优化的时候经常考虑的循环。

自然循环的定义是：

1）这个循环里a可以domniate所有的节点。

2）a domniate b,并且有一条边b 指向a。

3）包含这个回边的集合是最小集合。

具体的算法实现是：找到回边以后，把那些可以走到B的点加进来，直到A，这些节点和这些节点所在的边组在一起就是一个自然循环，具体实现的方法是进行深度优先搜索，先找到回边，然后逐步加入点和边。

两个循环的关系: 任意两个循环要么是嵌套的，要么不相交(可能有公共的入口结点)。内循环是指不包含任何其它循环的循环。

如果两个自然循环有相同的首结点，且两个循环不是一个嵌在另一个里面时，可以考虑将二者合并，当成是一个循环。

常用的代码优化方法

公共子表达式合并

如果表达式x op y先前已被计算过，并且从先前的计算到现在，x op y中的变量值没有改变，则x op y的这次出现就称为公共子表达式（common subexpression）

死代码删除

死代码(Dead-code)：其计算结果永远不会被使用的语句

常量传播

如果在编译时刻推导出一个表达式的值是常量，就可以使用该常量来替代这个表达式。该技术被称为 常量传播

循环不变计算优化

这个转换的结果是那些 不管循环多少次都得到相同结果的表达式（即循环不变计算，loop-invariant computation），在进入循环之前就对它们进行求值。

强度削弱

用较快的操作代替较慢的操作，如用 加 代替 乘 。（例：2*x ⇒ x+x）

删除归纳变量

对于一个变量x ，如果存在一个正的或负的常数c使得每次x被赋值时它的值总增加c ，那么x就称为归纳变量(Induction Variable)。在沿着循环运行时，如果有一组归纳变量的值的变化保持步调一致，常常可以将这组变量删除为只剩一个

有关LLVM

以前我们说，对于m种编程语言需要在n个机器上运行的情况，需要实现m*n个版本的编译器，而现代的编程语言使用前后端分离的思想来做，前端的m种语言只要转换成统一的中间表示，然后中间表示再针对n个后端做代码生成，这样将工作量缩小到了m+n。我接触到LLVM还是在学习TVM的时候，现在关于LLVM的介绍最好先把LLVM官方的Tutorial过一遍，其他的很多Tutorial知乎上太多了，这里就不再赘述了，讲一些与课程有关的部分。

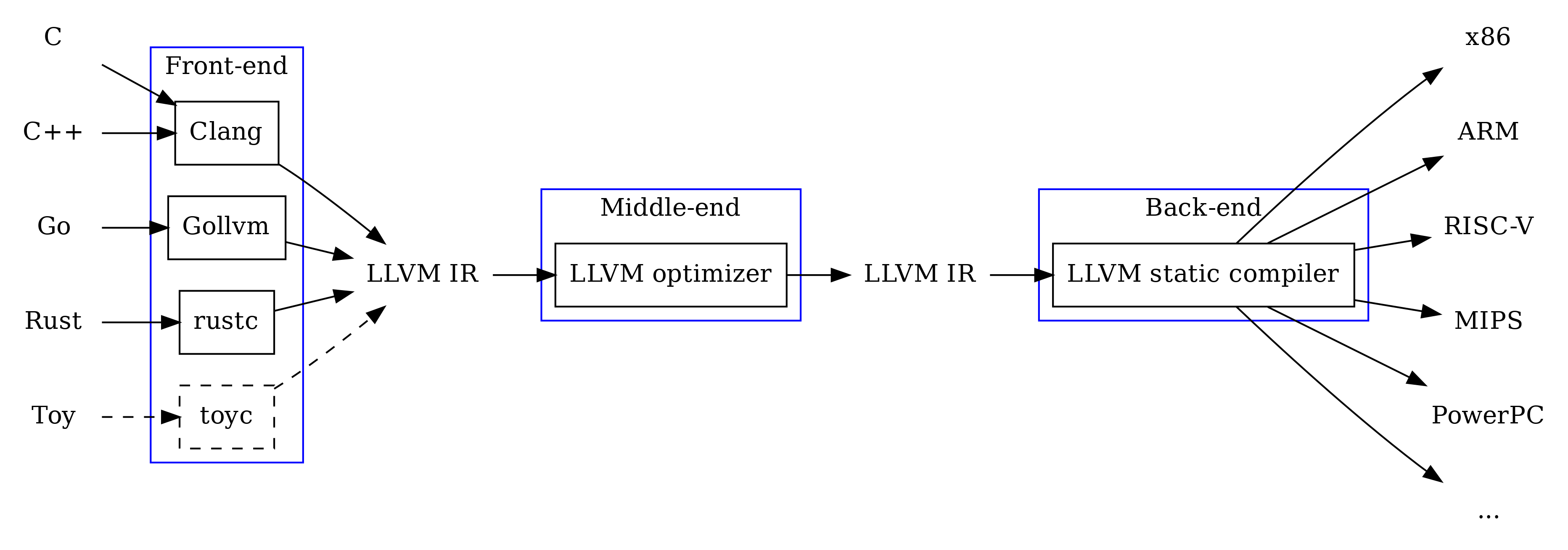
Value是一切的开始

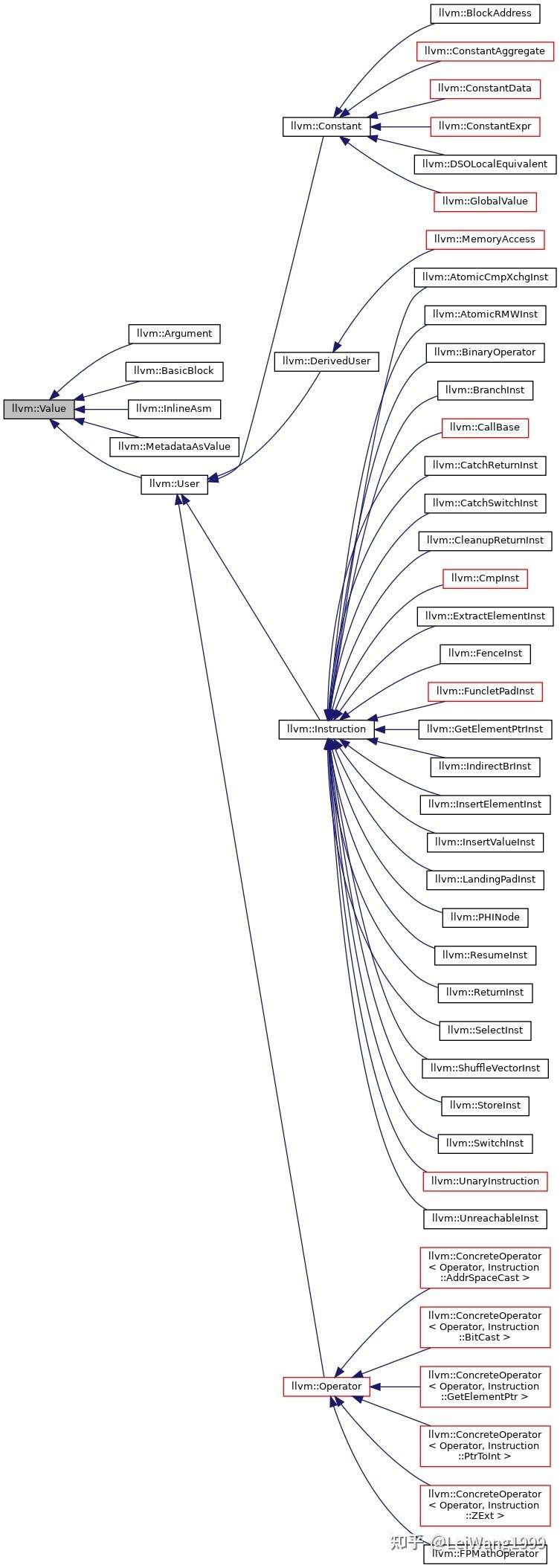
下图是LLVM由Value派生出来的类型之间的关系图，我们非常熟悉的BasicBlock、Argument直接继承自Value，而Instruction集成自User集成自Value，可以说在LLVM的架构中，几乎所有东西都是个Value。

举一个例子，我们用LLVM的IR手撸一段LLVM字节码来阐述一下Use和Value之间的关系：

; ModuleID = '0.user-value.bc'
target datalayout = "e-m:o-i64:64-f80:128-n8:16:32:64-S128"
target triple = "x86_64-apple-macosx10.15.0"

define dso_local i32 @main(){
    %1 = sub i32 0, 15;
    %2 = add i32 %1, 0;
    %3 = mul i32 %2, 2;
    ret i32 0;
}

不妨借助这一段字节码来简单的概括一下LLVM中间表示的语法：

• ModuleID 是用来唯一标示每一个字节码文件/模块的标识。然后在字节码文件里，;之后的一行的内容表示注释，和大部分汇编语言一样。
• 其次，如果字节码文件是从c/cpp源文件编译出来的，会有一个source_filename字段，表示字节码产生的源文件名。
• target datalayout 表示的是生成的代码需要对目标机器做的一些约束，用-分隔，比如e表示目标机器是小端格式的字节序（E表示大端）,比如S表示堆栈（Stack）是以128bit来对齐的。
• target triple 表示目标机器的信息，可以看到我使用的是x86架构的MacOS。
• 如下的文法是类C的，除了定义一个函数是define、声明一个函数是declare，关于这部分文法的具体内容可查看LLVM官方文档中的instruction reference，在写指令，声明函数的时候，可以加上一些可选项，例如在这里的dso_local是指变量和函数的的运行时抢占说明符，编译器可以假设标记为的函数或变量dso_local将解析为同一链接单元内的符号。即使定义不在此编译单元内，也将生成直接访问。

另外值得一提的是临时寄存器的命名，在LLVM的Module里面，clang 默认生成的虚拟寄存器是按数字顺序命名的，LLVM 限制了所有数字命名的虚拟寄存器必须严格地从 0 开始递增，且每个函数参数和基本块都会占用一个编号。所以，在我们刚才手写的字节码里，寄存器是以%1开始的，因为包含该段指令的基本块隐式地占用了一个寄存器编号0。

如果将原函数改写如下：

define dso_local i32 @main(){
    %0 = sub i32 0, 15;
    %1 = add i32 %0, 0;
    %2 = mul i32 %1, 2;
    ret i32 0;
}

进行可视的字节码到二进制字节码的转换：

$ llvm-as test00.ll -o test00.bc
llvm-as: test00.ll:7:5: error: instruction expected to be numbered '%1'
    %0 = sub i32 0, 15;

LLVM的字节码在内存里有两种形式，一种是可供人为阅读的文本格式的后缀名为ll的文件，另一种是二进制形式的后缀名为bc的文件，两者是等价的，将我们编写程序进行解析的时候，读入的是bc文件，而我们人为阅读是ll文件，两者可以通过 llvm-as 和 llvm-dis 命令相互转换。

如果我们显式的给基本块一个名称，则编译是可以正常通过的。

define dso_local i32 @main(){
  _entry:
  ; 显式地给基本块指定一个名称
    %0 = sub i32 0, 15
    %1 = sub i32 0, %0
    %2 = add i32 0, %1
    ret i32 %2
}

还是看到我们原来写的LLVM的字节码:

; ModuleID = '0.user-value.bc'
target datalayout = "e-m:o-i64:64-f80:128-n8:16:32:64-S128"
target triple = "x86_64-apple-macosx10.15.0"

define dso_local i32 @main(){
    %1 = sub i32 0, 15;
    %2 = add i32 %1, 0;
    %3 = mul i32 %2, 2;
    ret i32 0;
}

这部分代码明显是可以使用删除归纳变量的优化方法进行优化，将临时寄存器%2删除，并且还需要将%3的右边的%2替换成%1，为了实现该技术就需要知道寄存器之间的依赖关系，所以有use-def chain和def-use chain技术。use-def 链是指被某个 User 使用的 Value 列表，def-use 链是使用某个 Value 的 User 列表。实际上，LLVM 中还定义了一个 Use 类，Use 就是上述的使用关系中的一个边。也就是说是一个 Value->Use->User 这样的一个概念。

假设我们的Inst是%2 = add i32 %1, 0;，对该指令的操作数进行遍历：

for (auto op_it = I.op_begin(); op_it != I.op_end(); ++op_it){
    Value * Operand = *op_it;
}

我们得到拿到的Operand的结果应该是 %1和0。

对user进行遍历：

for (auto user_it = I.user_begin(); user_it != I.user_end(); ++user_it){
    User * InstUser = *user_it;
}

拿到的应该是%3 = mul i32 %2, 2这一条指令，或者是%3这个Value，但是根据StackOverflow的llvm get operand and lvalue name of an instruction这个帖子的描述，在ll文件里类似%<num>是writer在打印阶段加上去以方便人类阅读，实际上这样的临时寄存器在Module里面并不具有名字，我们没有办法把诸如%2这样的临时寄存器的名字进行输出。

静态单赋值(Single Static Assignment)

此外，上述的代码中，所有的表达式都是静态单赋值(Static Signle Assignment)，对这部分的内容部分摘自这篇文章。

In compiler design, static single assignment form (often abbreviated as SSA form or simply SSA) is a property of an intermediate representation (IR), which requires that each variable is assigned exactly once, and every variable is defined before it is used.
————————————————

Wiki

从上面的描述可以看出，SSA 形式的 IR 主要特征是每个变量只赋值一次。相比而言，非 SSA 形式的 IR 里一个变量可以赋值多次。例如如下这段代码：

y := 1
y := 2
x := y

显然，我们一眼就可以看出，上述代码第一行的赋值行为是多余的，第三行使用的 y 值来自于第二行中的赋值。对于采用非 SSA 形式 IR 的编译器来说，它需要做下文中讲到的数据流分析方法之到达-定义分析，来确定选取哪个表达式的 的y 值。但是对于 SSA 形式来说，就不存在这个问题了。如下所示，经过SSA处理后的代码是：

y1 := 1
y2 := 2
x1 := y2

显然，我们不需要做数据流分析就可以知道第三行中使用的 y 来自于第二行的定义，这个例子很好地说明了 SSA 的优势。除此之外，还有许多其他的优化算法在采用 SSA 形式之后优化效果得到了极大提高。甚至，有部分优化算法只能在 SSA 上做。

但是，我们观察Clang吐出来的LLVM IR，可以发现这并不是真正的SSA，比如在 LLVM Tutorial里面的7. Kaleidoscope: Extending the Language: Mutable Variables这一章节，提到的对于这样的一个函数：

int foo(int x, bool cond) {
  int inc;
  if (cond) {
    inc = 1;
  } else {
    inc = -1;
  }
  return x + inc;
}

Clang的前端通过``clang -Xclang -disable-O0-optnone -O0 -emit-llvm -S foo.c` 生成的LLVM IR是：

; Function Attrs: nounwind uwtable
define i32 @_Z3fooib(i32 %x, i1 zeroext %cond) #0 {
entry:
  %x.addr = alloca i32, align 4
  %cond.addr = alloca i8, align 1
  %inc = alloca i32, align 4
  store i32 %x, i32* %x.addr, align 4
  %frombool = zext i1 %cond to i8
  store i8 %frombool, i8* %cond.addr, align 1
  %0 = load i8, i8* %cond.addr, align 1
  %tobool = trunc i8 %0 to i1
  br i1 %tobool, label %if.then, label %if.else

if.then:                                          ; preds = %entry
  store i32 1, i32* %inc, align 4
  br label %if.end

if.else:                                          ; preds = %entry
  store i32 -1, i32* %inc, align 4
  br label %if.end

if.end:                                           ; preds = %if.else, %if.then
  %1 = load i32, i32* %x.addr, align 4
  %2 = load i32, i32* %inc, align 4
  %add = add nsw i32 %1, %2
  ret i32 %add
}

可以观察到到局部变量都在函数的最开头（entry block）有对应的alloca来“声明”它们——申请栈上空间。后面赋值的地方用store、取值的地方用load指令，就跟操作普通内存一样。因为LLVM IR虽然是SSA形式的，但如果所有生成LLVM IR的前端都要自己计算好如何生成SSA形式，对前端来说也是件麻烦事。

而经过mem2reg之后它才真正进入了SSA形式，在终端我们可以通过opt -S -mem2reg -o foo.m2r.ll foo.ll这一命令生成完全的SSA形式的IR：

; Function Attrs: nounwind uwtable
define i32 @_Z3fooib(i32 %x, i1 zeroext %cond) #0 {
entry:
  %frombool = zext i1 %cond to i8
  %tobool = trunc i8 %frombool to i1
  br i1 %tobool, label %if.then, label %if.else

if.then:                                          ; preds = %entry
  br label %if.end

if.else:                                          ; preds = %entry
  br label %if.end

if.end:                                           ; preds = %if.else, %if.then
  %inc.0 = phi i32 [ 1, %if.then ], [ -1, %if.else ]
  %add = add nsw i32 %x, %inc.0
  ret i32 %add
}

可以看到进入SSA形式后的LLVM IR里，那些局部变量就变成了普通的SSA value，而不再需要alloca/load/store了。

所以我们注意到，在我们的作业2和作业3里，首先都会把clang生成的LLVM IR通过一个createPromoteMemoryToRegisterPass转化成真正的SSA形式，这样才可以得到Phi节点的相关信息。

/// Transform it to SSA
Passes.add(llvm::createPromoteMemoryToRegisterPass());

关于mem2reg的更多内容与算法实现，请移步此文。

以下述代码为例讲述如何构造SSA，程序在函数体结尾会将x的值赋给y。

if(x < 0)
    x = 2;
else
    x = 0;
int y = x;

那么在代码优化时，我们并不知道赋值于y的值是多少。所以引进了 Φ(Phi) 函数，并重命名了变量

// 注：其中的x1，x2的数字都是下标。其本质上还是x
if(x < 0)
    x1 = 2;
else
    x2 = 0;
int y = Φ(x1, x2);

从之前的LLVM IR的例子里能发现 Φ(Phi)的指令：%inc.0 = phi i32 [ 1, %if.then ], [ -1, %if.else ]。它会根据当前的basicblock（因为phi肯定是basicblock最前面的指令）之前执行的是哪一个basicblock来确定需要产生的值。

总结：三步走战略

• 找出各个内含变量定值的基础块，以及这些基础块所对应的支配边界。有关支配边界，在之后会讲述。

• 插入PHI节点： PHI节点要插在控制流图的汇聚点处（joint point), 只要在汇聚点之前的分支中有针对某个变量的修改， 就需要在该汇聚点插入针对该变量的PHI节点。 PHI节点的操作数是分支路径中重新定义的变量。

• 变量重命名： 在插入PHI节点后，SSA中所有针对变量的定义就具备了，接下来就依次在定义处重命名变量，并替换对应的变量使用处。

• 我们需要将 Φ 函数正确插入至代码块中。所以最关键的问题是 —— 插入至何处？插入至 各个变量定值所在的基础块集合 的 所有支配边界 。详见下面的算法。

Use-Def Chain

LLVM是如何建立起来Value之间的def-use或者是use-def关系的呢？举一个知乎上的例子来说，假如我们要创建一个Add指令，BinaryOperator::CreateAdd(Value *V1, Value *V2, const Twine &Name)，这条新创建的Add（BinaryOperator）指令是如何跟它的两个输入（V1、V2）建立起def-use/use-def联系的呢？请看下面的代码：

class Value {
  void addUse(Use &U) { U.addToList(&UseList); }

  // ...
};

class Use {
  Value *Val;
  Use *Next;
  PointerIntPair<Use **, 2, PrevPtrTag> Prev;

  // ...
};

void Use::set(Value *V) {
  if (Val) removeFromList();
  Val = V;
  if (V) V->addUse(*this);
}

Value *Use::operator=(Value *RHS) {
  set(RHS);
  return RHS;
}

class User : public Value {
  template <int Idx, typename U> static Use &OpFrom(const U *that) {
    return Idx < 0
      ? OperandTraits<U>::op_end(const_cast<U*>(that))[Idx]
      : OperandTraits<U>::op_begin(const_cast<U*>(that))[Idx];
  }
  template <int Idx> Use &Op() {
    return OpFrom<Idx>(this);
  }
  template <int Idx> const Use &Op() const {
    return OpFrom<Idx>(this);
  }

  // ...
};

class Instruction : public User,
                    public ilist_node_with_parent<Instruction, BasicBlock> {
  // ...
};

class BinaryOperator : public Instruction {
  /// Construct a binary instruction, given the opcode and the two
  /// operands.  Optionally (if InstBefore is specified) insert the instruction
  /// into a BasicBlock right before the specified instruction.  The specified
  /// Instruction is allowed to be a dereferenced end iterator.
  ///
  static BinaryOperator *Create(BinaryOps Op, Value *S1, Value *S2,
                                const Twine &Name = Twine(),
                                Instruction *InsertBefore = nullptr);

  // ...
};

BinaryOperator::BinaryOperator(BinaryOps iType, Value *S1, Value *S2,
                               Type *Ty, const Twine &Name,
                               Instruction *InsertBefore)
  : Instruction(Ty, iType,
                OperandTraits<BinaryOperator>::op_begin(this),
                OperandTraits<BinaryOperator>::operands(this),
                InsertBefore) {
  Op<0>() = S1;
  Op<1>() = S2;
  init(iType);
  setName(Name);
}

BinaryOperator *BinaryOperator::Create(BinaryOps Op, Value *S1, Value *S2,
                                       const Twine &Name,
                                       Instruction *InsertBefore) {
  assert(S1->getType() == S2->getType() &&
         "Cannot create binary operator with two operands of differing type!");
  return new BinaryOperator(Op, S1, S2, S1->getType(), Name, InsertBefore);
}

从BinaryOperator的构造器开始看，会看到里面有这样一段看起来很有趣的代码：

Op<0>() = S1;
Op<1>() = S2;

追溯源头会来到Use::set(Value *V)，这里就借助Use对象来把def与use的双向引用给联系起来了。

构造SSA

支配树与支配边界(Dominator Frontier )

在生成SSA的时候，需要计算在何处插入正确的 Φ (phi-function) ，一种方法是在所有有多个前驱的Basic Block的开头插入 Φ-node*，但是这种方法会插入很多的无用的 *Φ-node ，有很多 Φ-node 的参数都是相同的一个定义。这样得到的 SSA 形式的 IR，占用过多的内存，增加了计算的开销。任何使用该SSA进行代码分析或者优化的过程都会浪费很多计算资源。为了减少 Φ-function 的数量，首先想到的方法就是确定插入 Φ-function 的精确位置。

龙书中，关于Dominance的定义如下：

如果每一条从流图的入口结点到结点 n 的路径都经过结点 d, 我们就说 d 支配（dominate）n，记为 d dom n。请注意，在这个定义下每个结点都支配它自己。-《编译原理》
d dom i if all paths from entry to node i include d.

老师的课件里给出的控制节点的描述如下：

可知， 如果A 支配 B，那么不可能不经过A就可以从入口处到达B，一个基础块永远 支配自己（ 严格支配/真控制 排除支配自己这种情况）。

直接控制的人话表述应该是：直接支配节点(Immediate Dominator)： 从入口处节点到达节点n的所有路径上，结点n的 最后一个支配节点 称为 直接支配节点。

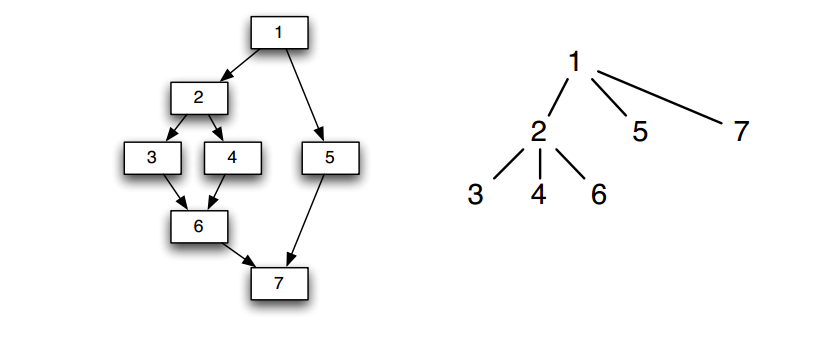
由直接控制节点组成的树就是控制树，左图所示的控制流图转化为控制树如右图所示。

在构造 SSA 过程中，还有另外一个概念很重要，就是支配边界（dominance frontier）。支配边界直观理解就是当前结点所能支配的边界（并不包括该边界）。

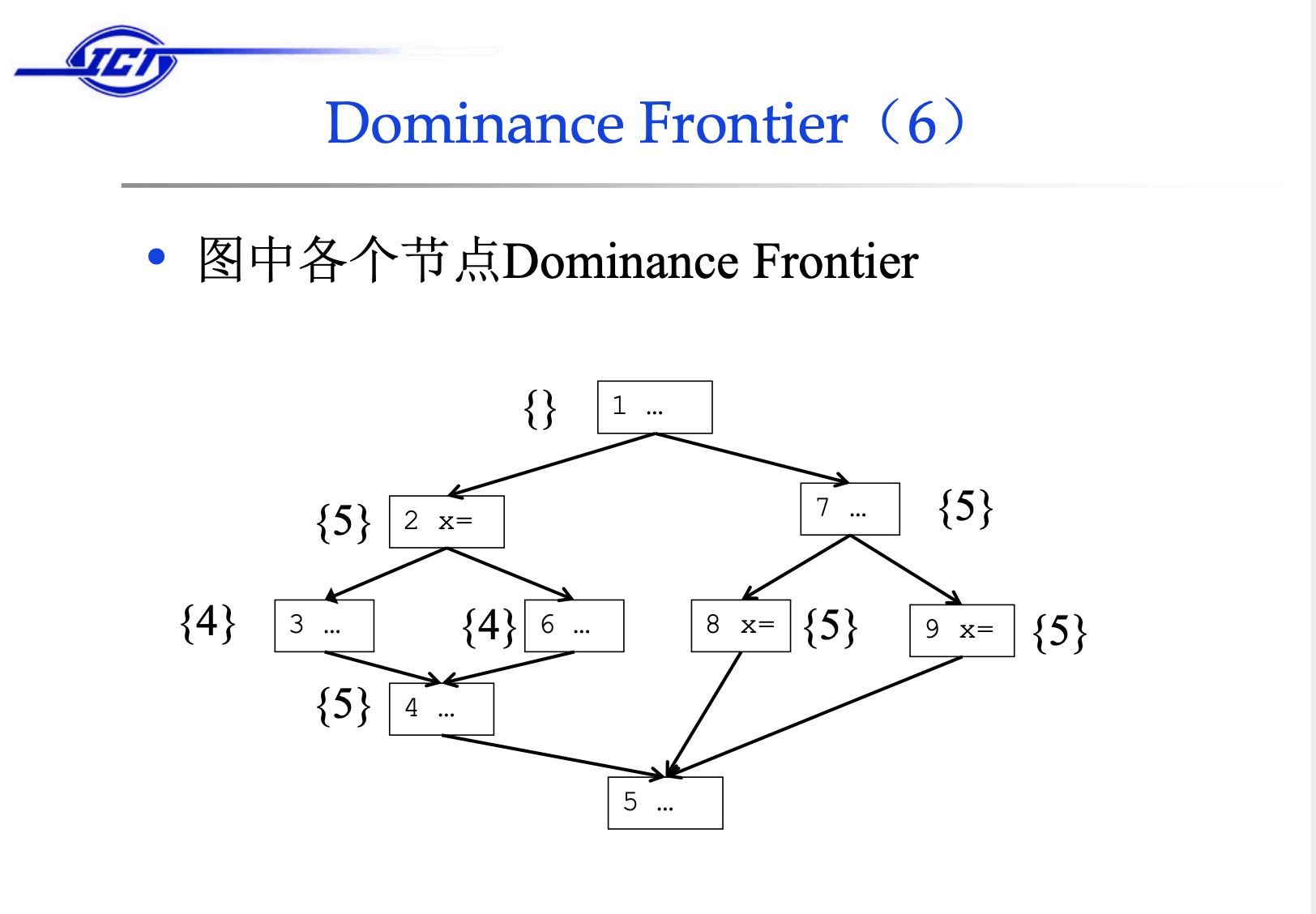
上图中，基本块1控制所有的基本块，所以他没有控制边界；基本块2控制2、3、6、4、但是不能控制4的后继节点5，所以5是其控制边界。那么支配边界（dominance frontier）的的意义在哪里呢？

In SSA form, definitions must dominate uses.

下面给出的是wiki中的描述，支配边界确定了 Φ-function 的插入位置。由于每个definition支配对应的uses，所以如果达到了definition所在block的支配边界，就必须考虑其他路径是否有其他相同variable的定义，由于在编译期间无法确定会采用哪一条分支，所以需要放置 Φ-function。

Dominance frontier capture the precise places at which we need Φ-function: if the node A defines a certain variable, then that definition and that definition alone(or redefinitions) will reach every node A dominates.

Only when leave these nodes and enter the diminance frontier must we account for other flows bringing in other definitions of the same variable.

考虑下面的图示， 结点 1 定义了一个值x := 3，这个值可以传播到结点 1 所支配的所有结点（除了 entry 的所有结点）中，只有在到达结点 1 的支配边界的时候，才需要考虑其他路径是否有对 x 的定义并且插入适当的 Φ-function。

虽然从结点1的角度来看，它支配结点（例如9，10，11）可能会用到x:=3，但并不意味着这些节点里不需要插入ϕ 节点，因为节点1支配的节点里也会存在对于x的def，而他们的控制边界也可能属于节点1的支配节点。

结点 5 定义了值x := 4，结点 5 没有支配结点并且结点 9 就是结点 5 的支配边界，在这里需要考虑从从其他路径传播到此的对变量 x 的其他定义，也就是结点 1 中的定义 x := 3。所以在结点 9 需要插入一个关于变量 x 的 Φ-function。同理在结点 10 的开头也需要插入一个 Φ-function，另外由于 Φ-function 会产生新的定义，所以也需要在结点 9 的支配边界结点 11 的开头插入 Φ-function。

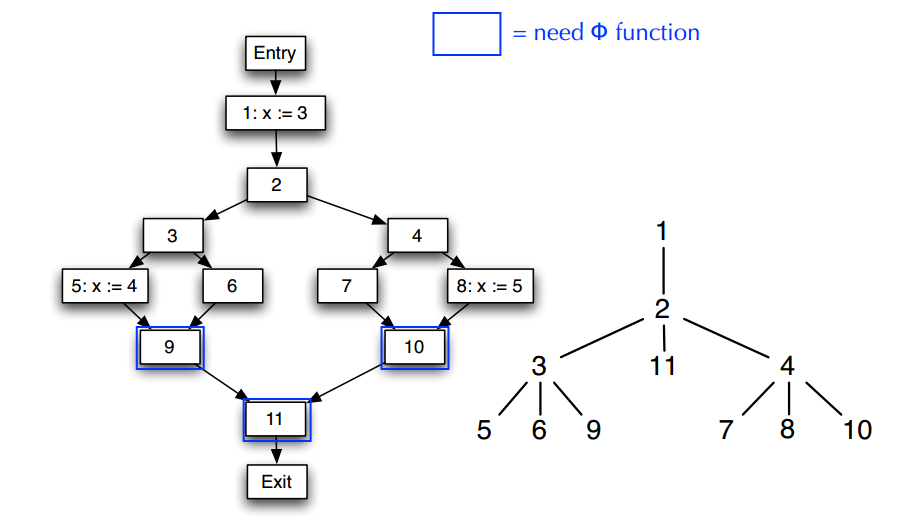
前文中讲到，如果要确定支配边界的话，需要先构造出支配树。

计算支配树最有名的一个算法是 Lengauer-Tarjan algorithm ，这个算法有接近线性的复杂度，但是不是很容易理解。当然也有其他方法，例如最简单的方法，就是对于 CFG 中某一个点 A，获取根到结点 A 的一条路径，然后依次删除路径上的某一个点，然后检查结点 A 是否还能从根节点到达。如果删除某个点后，结点 A 从根节点不可达，那么这个点支配结点 A。该方法简单，知道支配性的都会明白该算法，但是该算法复杂度很高，接近 O(n^4) 的复杂度。

相比之下，另外一种迭代数据流分析的方法更容易理解，复杂度只有 O(n^2) ，几乎现在所有编译方面的书籍都是介绍的这种方法。老师的课件里给出的计算控制节点的算法正是这种算法，在龙书中也有描述：

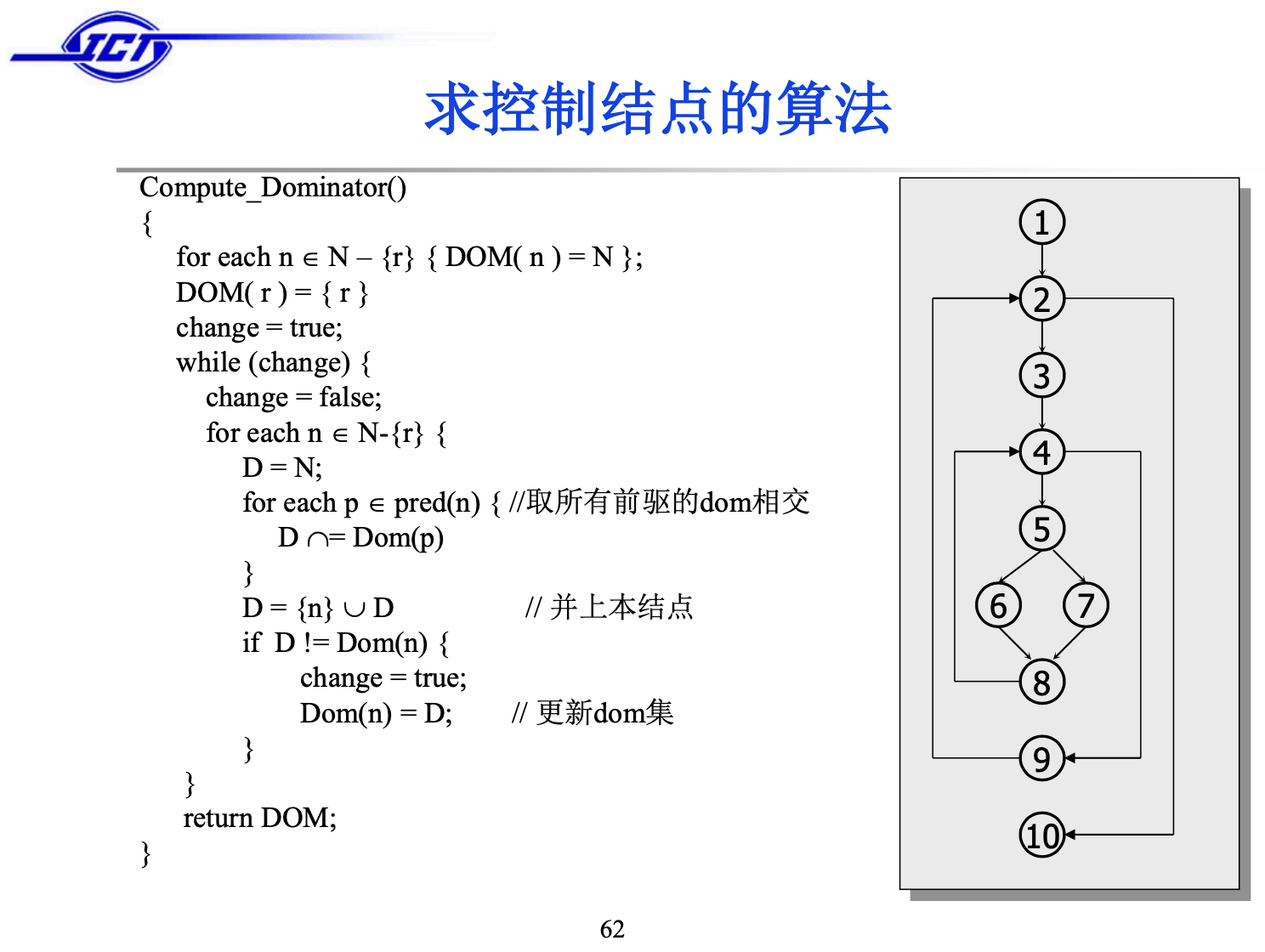
该问题其实可以抽象成一个数据流分析问题，在数据流分析这一块有简单的讲，CSCD70里的例子已经讲的非常形象了：

首先，entry point的out[1]设置为本身，然后其他所有的basicblock的out[b]变成所有的basic block，接着深度优先遍历所有的节点套用图中的transfer function就可以得出他的dominator了。

根绝每个节点的dominator，可以得出直接控制节点就是倒数第一个控制节点（拍出自身的话），控制树也就可以得到。

计算控制边界的算法：

引入phi节点

下面介绍如何通过已经计算好的控制边界来引入ϕ节点，先给出这个算法的伪代码：

从伪码来看，首先我们需要将workList和everOnWorkList初始化为对X赋值过的基本块，所以如下的控制流图经过算法的初始化后三个数组的内容如下。

然后进入循环之后，首先我们从workList里移除节点1，但是节点1的控制边界是空集，所以循环跳过，接下来移除节点8，8的控制边界是9，因为9不在alreadyList里，所以我们需要在9这里插入一个phi节点，并且把9插入worklist里,因为9不再everOnWorkList里，所以需要吧9插入everOnWorkList和workList内部。

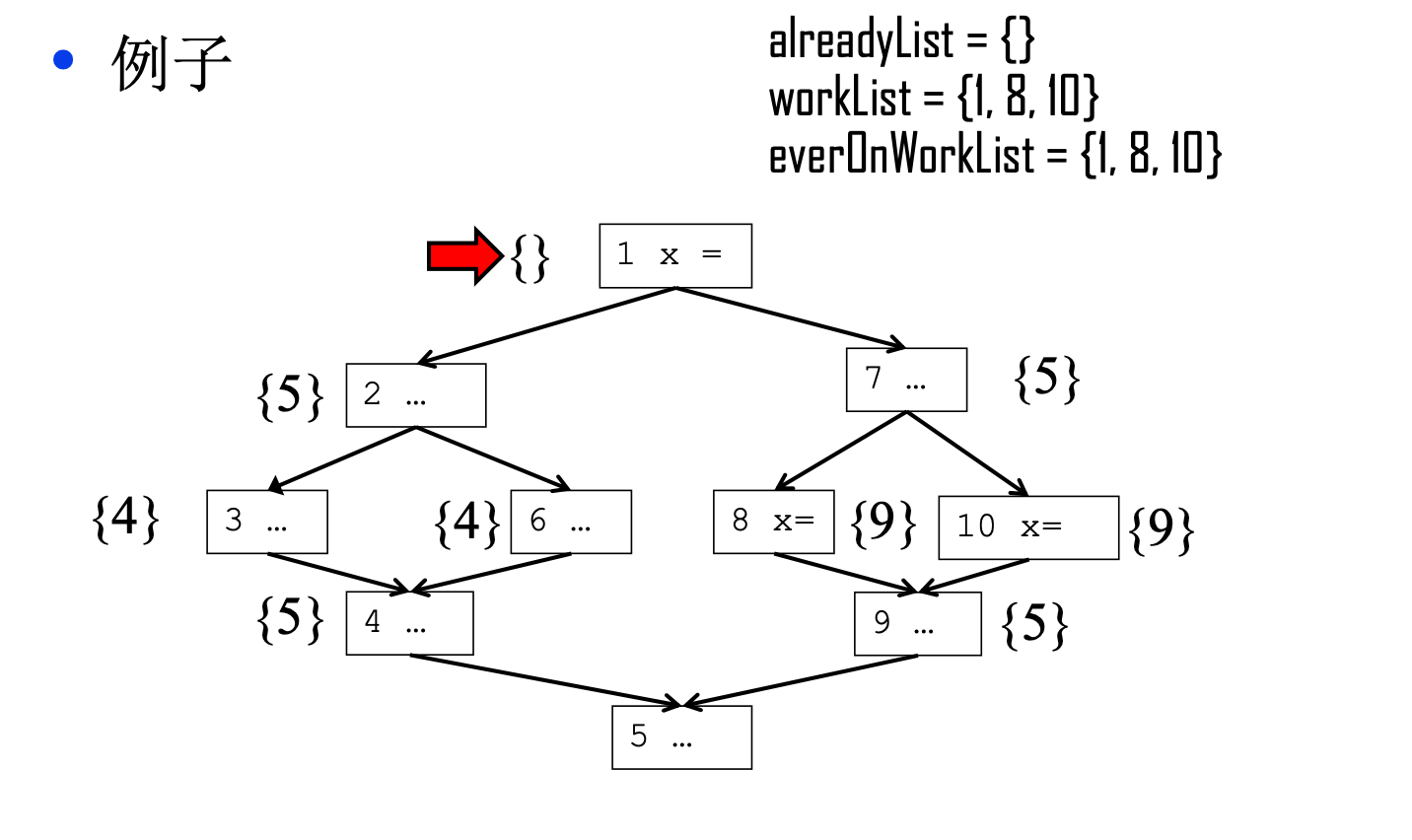
此时，alreadyList的内容是{9}，workList的内容是{10,9}, everonWorkList的内容是{1,8,10,9}。

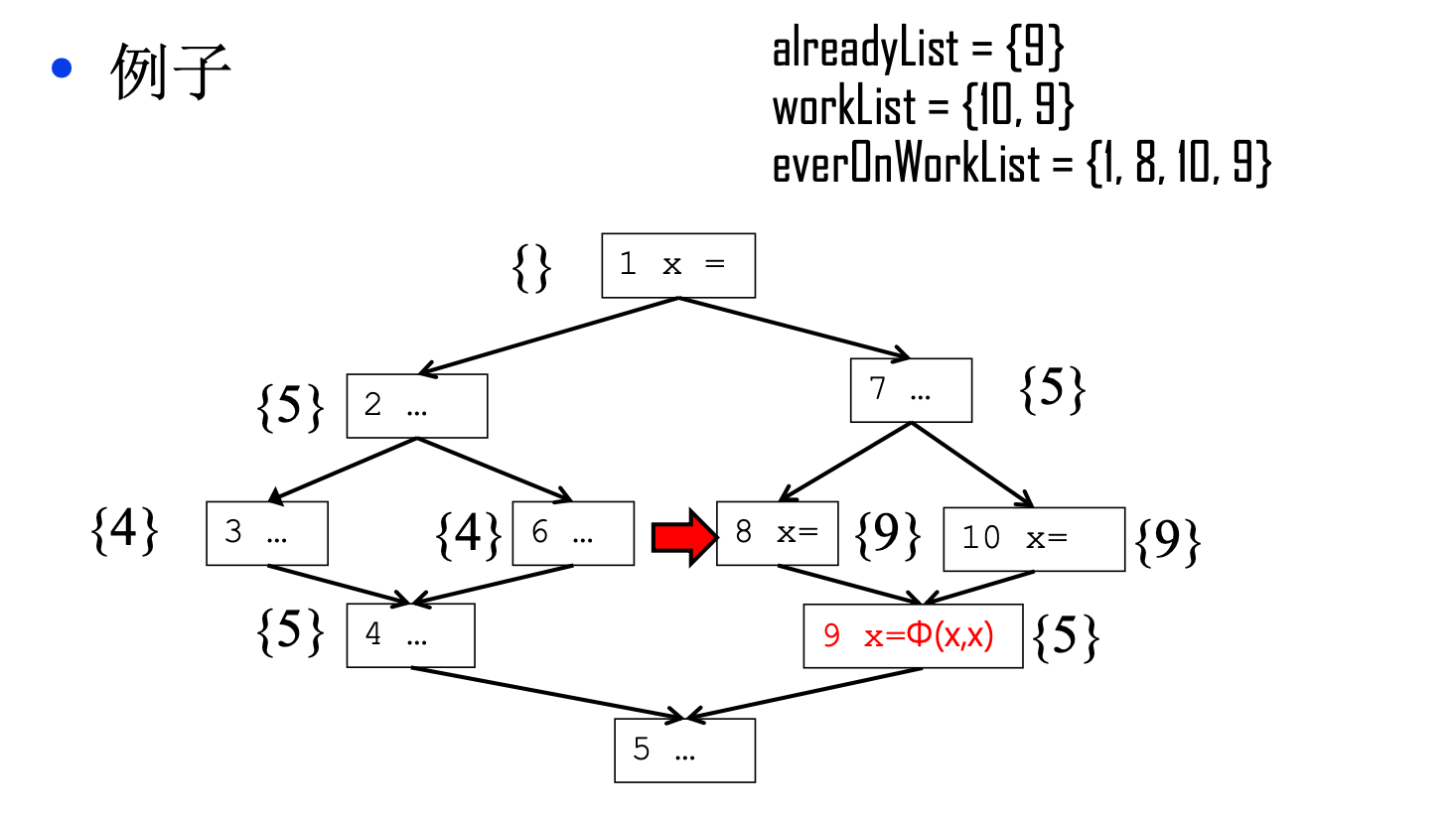
接着是从workList里弹出节点10，他的控制边界也是9，但因为9在alreadyList和everOnWorkList内，所以循环跳过，接着从workList里弹出9，9的控制边界是5，算法会运行到这一步：

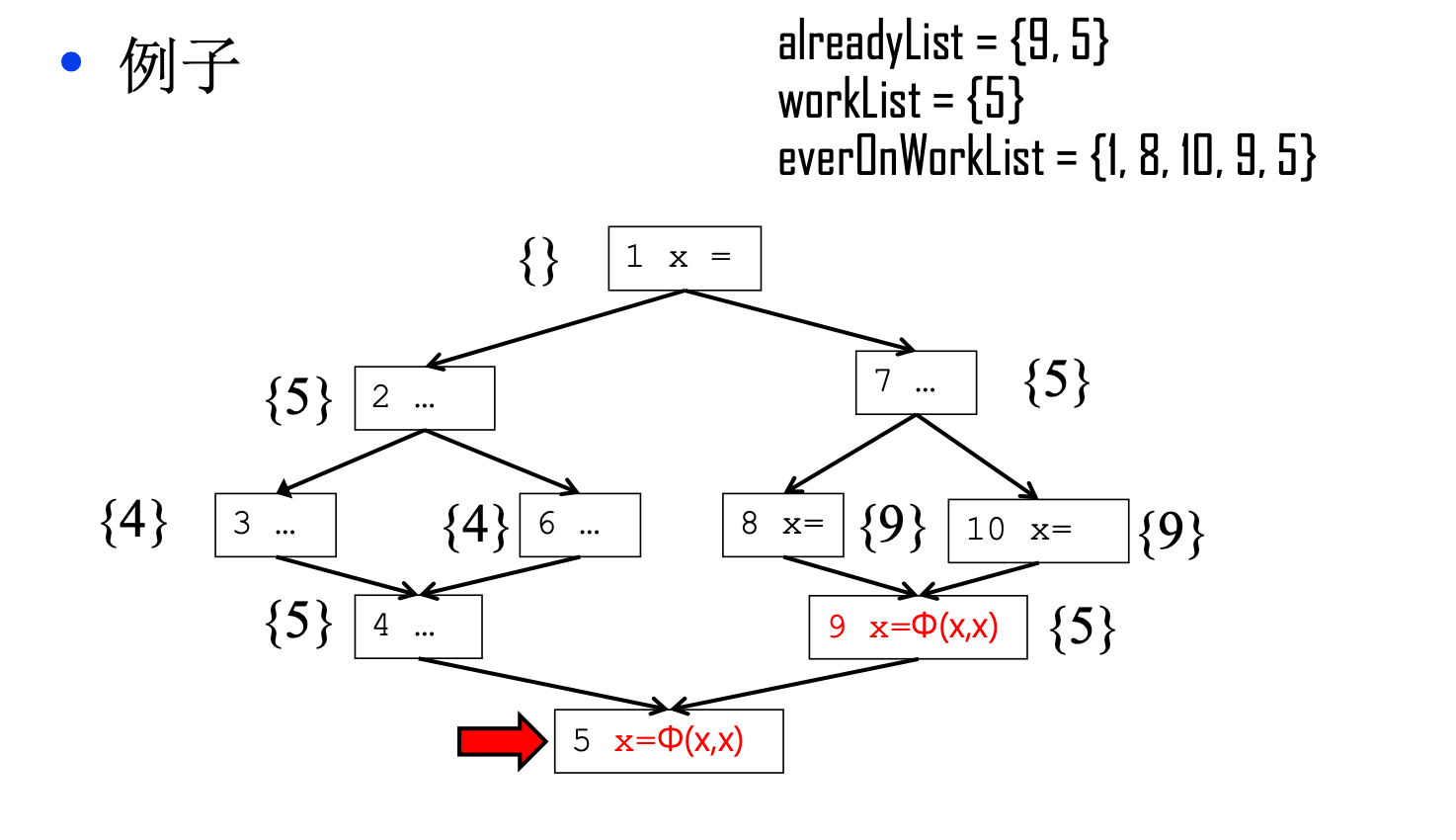
接着弹出5，不清楚5之后是什么情况的话，这里就是算法运行最后的结果，可以看到我们已经在合适的地方插入了phi节点，但是phi节点内的变量没有重命名。

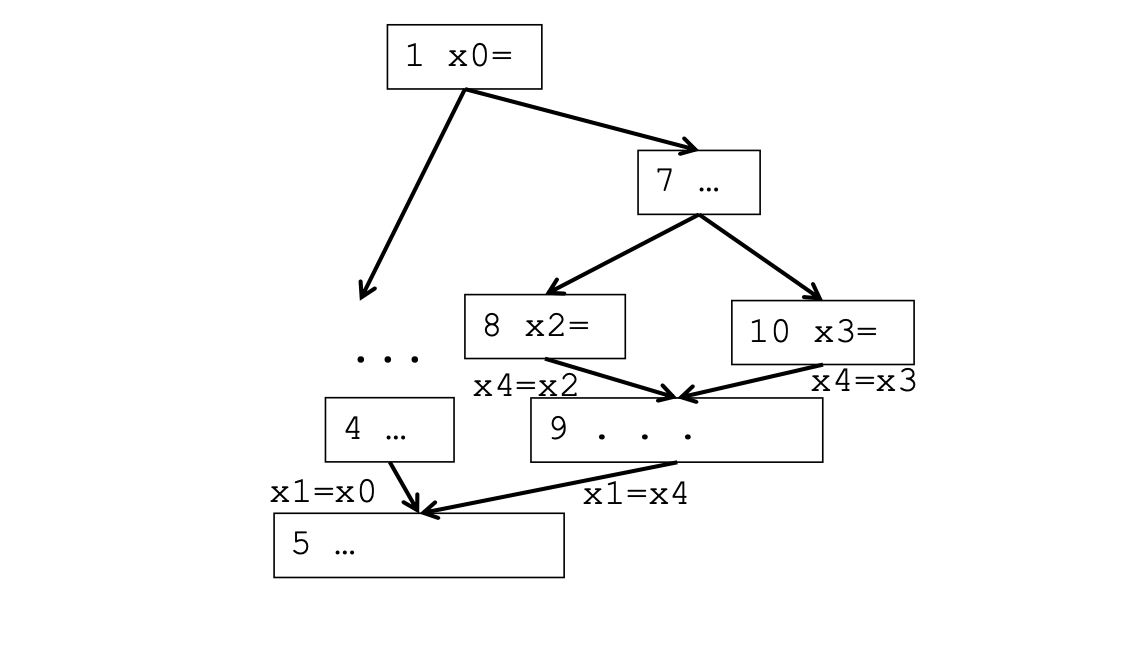
重新命名变量

重新命名变量的算法如下，其是对控制树进行先序遍历，因为算法运行的过程太过繁琐，模拟起来太麻烦了就不写了！其实就是对重复出现的变量换角标。

翻译成可执行代码

在前驱节点插入copy语句、优化不必要的copy语句。

数据流分析(Dataflow Analysis)

与Dataflow Analysis对应的是Local Analysis，Local Analysis做的是基本块内部的优化，比如Value Numbering。

数据流分析更注重在分析不同的基本块之间的影响，比如说可以做，常量合并、通用子表达式删除和死代码删除，该技术是许多静态程序分析优化方法的基础。

在讲述具体的分析算法之前，需要先阐述一下数据流分析的一些模式。

这些数据流值是和具体的数据流问题相关的，有可能是当前程序点的定值信息，也有可能是可用表达式信息，这些信息标识着该程序内含的一些属性。

我们把每个语句s之前和之后的数据流值分别记为IN[s]和OUT[s]。数据流问题就是对一组约束求解，得到所有IN[s]和OUT[s]的结果。每个语句s都约束了in和out这两个数据流值之间的关系，这种约束关系叫做传递函数(transfer function)，由f来表示。

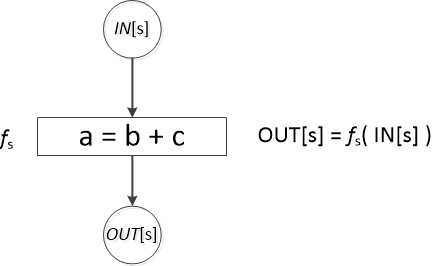
传递函数也有两种不同的风格：数据流信息可能沿着执行路径向前传播，或者沿着程序路径逆向流动，相应的就有前向(forward)数据流问题和后向(backward)数据流问题。

Forward data-flow analysis, Information at a node is based on what happens earlier in the flow graph.
Backward data-flow analysis, Information at a node is based on what happens later in the flow graph.

对于前向数据流问题，一个程序语句s的传递函数以语句前程序点的数据流值作为输入，并产生出语句之后程序点对应的新数据流值。例如到达定值就是前向数据流问题。
$$
OUT[s] = f(IN[s])
$$

对于后向数据流问题，一个程序语句s的传递函数以语句后的程序点的数据流值作为输入，转变成语句之前程序点的新数据流值。例如活变量分析就是后向数据流问题。
$$
IN[s] = f(OUT[s])
$$

所有的数据流分析的结果都具有相同的形式：对于程序中的每个指令，它们描述了该指令每次执行时必然成立的一些性质。

所以，面对一个数据流分析问题，我们要思考的内容有：

• Direction: forward or backward
• Value:
• Meet operator:union or intersect or plus …
• Top Element:
• Bottom Element:
• Boundary condition: start/entry node
• Initialization for internal nodes.
• Finite descending chain?
• Transfer function

之前讲到的，求解控制节点的算法也可以视作一个数据流分析问题，他的Direction是forward，Value是Basic blocks，meet operator 是 intersect，Top是all basicblocks, Bottom Element 是 empty set，对于Boundary condition，out[start]=start，

到达-定值（Reaching Definitions）

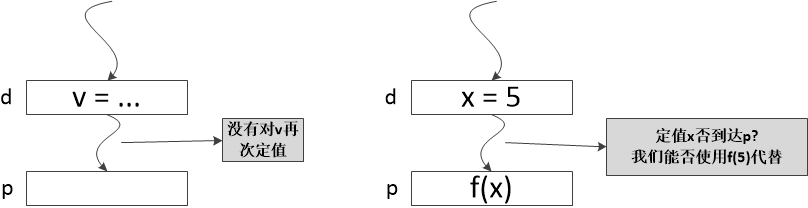
“到达-定值”是最常见的和有用的数据流模式之一。编译器能够根据到达定值信息知道 x 在点 p 上的值是否为常量，而如果 x 在点 p 上被使用，则调试器可以指出x是否未经定值就被使用。

如果存在一条从紧随在定值 d 后面的程序点到达某一个程序点 p 的路径，并且在这条路径上 d 没有被“杀死”，我们就说定值 d 到达程序点 p 。如果在这条路径上有对变量x的其他定值，我们就说变量 x 的这个定值（定值 d ）is killed。

这样的定义听上去非常的拗口，根据CSCD70课程里讲述的内容，到达定值应该是：

每一个赋值语句都是一个definition，这个definition是否能到达程序点p，就是到达定值的定义。

到达定值的应用主要有：

• 创建use/def链
• 常量传播
• 循环不变量外提

首先，我们定义两个函数，他们分别表示：

• gen[n] :节点 n 产生的定值（假设一个语句节点至多一个定值）
• kill[n] :节点 n“杀死”的定值

则对于一个definition，他的kill和gen函数产生的内容是这样的：

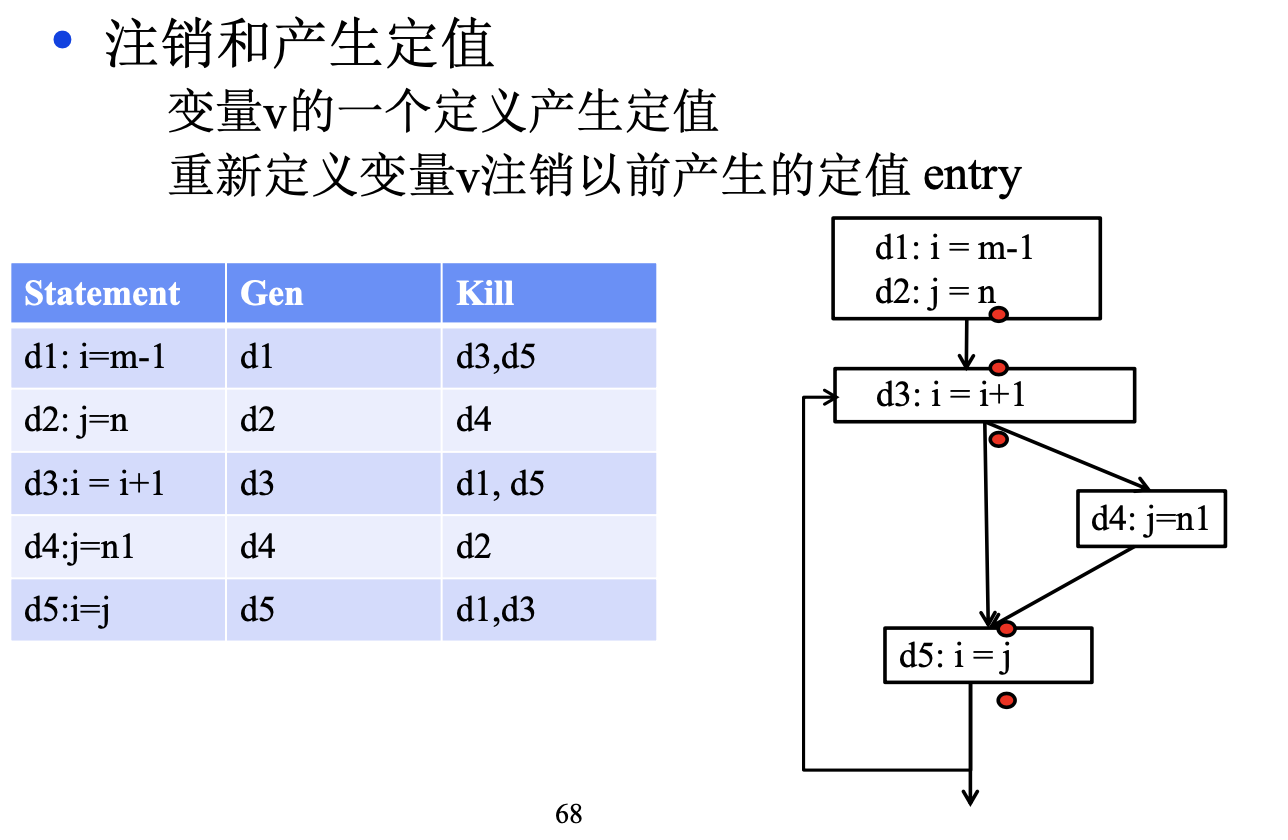
到达定值的传递方程：

对于到达定值来说，只要一个定值能够沿着至少一条路径到达某个程序点，就说这个定值到达该程序点。所以控制流方程的交汇运算时并集，但是对于其他一些数据流问题交汇运算时交集，例如可用表达式。

最后是编译原理中的，到达定值运算数据流方程的迭代求法：

可用表达式分析(available expressions)

例如有如下的代码：

int main(){
  int a = 1, b = 2, c = 3;
  int x = a+b+b+b+b;
  int y = a+b+b+b+b;
  int z = a+b+b+b+b;
  return 0;
}

a+b+b+b+b在y点和z点就是一个可用表达式，不进行优化的话该表达式将会被计算三次，所以我们编译优化的过程中要发现这一类的可用表达式。

定义：表达式x+y在点p可用:如果从初始结点到p 的任意路径上都计算x+y，并且在最后一个这样的计算和p之间没有对x或y的赋值。

表达式x+y产生:如果它计算x+y。

表达式x+y被注销:如果x或y被赋值(或可能赋值)。

老师的课件里给出的可用表达式的计算例子如下：

同样，我们使用定值分析也需要定义gen和kill函数，这里把in和out一并给上：

in[B]:块B开始点的可用表达式集合

out[B]:块B结束点的可用表达式集合

e_gen[B]:块B生成的可用表达式集合

e_kill[B]:U中被块B注销的可用表达式集合

他的数据流方程：

注意这里和之前的到达定值不一样，取得是交集。

具体的算法实现如下：

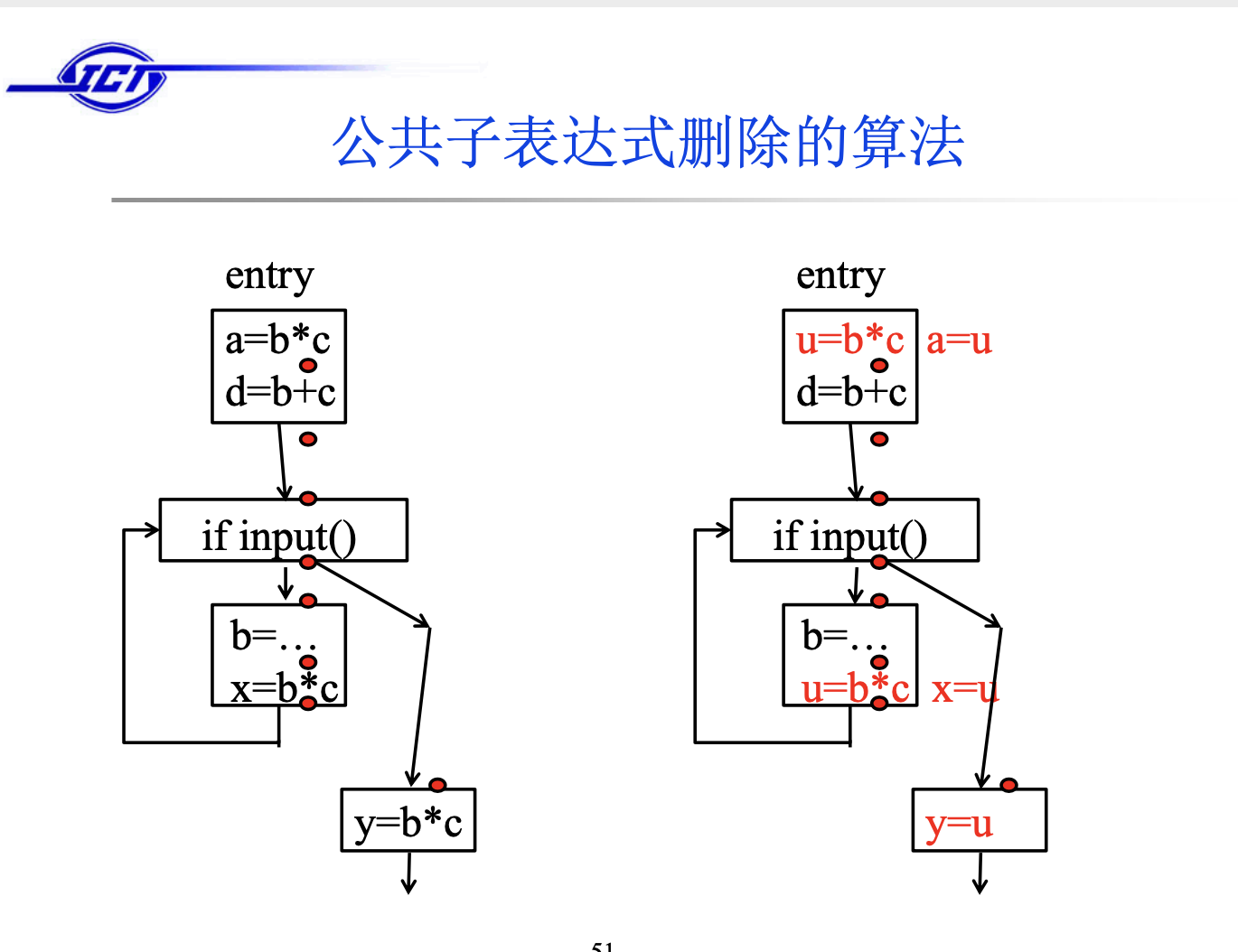
有了到了某个程序点的可用表达式信息，我们就可以实现公共子表达式删除，具体的流程是：

对每个形如x := y + z(+表示一般的算符)的语句s，如果 y + z在s所在块的开始点可用，且在该块中s前没有y和z的定值 ，则执行下面的步骤:

(1) 为了寻找到达s所在块的y + z的计算，顺着流图的边，从该块开始反向搜索，但不穿过任何计算y + z的块。在遇到的每个 块中，y + z的最后一个计算是到达s的y + z的计算。

(2) 建立新变量u

(3) 把(1)中找到的每个语句w := y + z用下面的两个语句代替 u := y + z 和w := u

(4) 用x := u代替语句s

算法的实现结果如下图：

活跃变量（Live Variable）

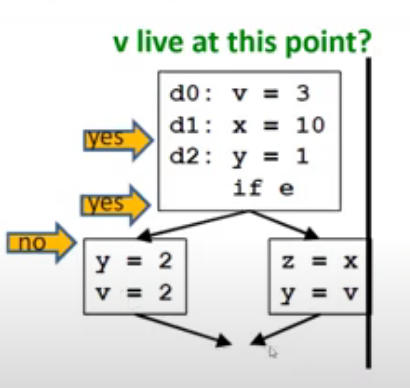
定义：A variable v is live at point p if the value of v is used along some path in the flow graph staring at p otherwise the variable is dead.变量v在程序点p活跃如果存在从p到exit的程序执行路径，v在该路径上被使用且v未被重新定义。

比如下面这个例子，对于变量v在前两个p点处都存在从p点到exit的路径，而且在该路径上都被使用了，所以变量v在这两个点是活跃的。但是在第三个p点到exit的路径上，v被重新定义了，所以在该点，v是不活跃的。

活跃变量的主要用途有：

• 删除死代码
• 为基本块分配寄存器

同样的，对于活跃变量定义的数据流方程：

in[B]:块B开始点的活跃变量集合

out[B]:块B结束点的活跃变量集合

def[B]:块B中无二义定值且在该定值前没有引用的变量集

use[B]:块B中可能引用且在该引用前没有定值的变量集

数据流分析框架

在上述的几个数据流分析的问题中，显然可以发现它们处理问题的方法存在一个类似的模式，数据流分析框架就是将这些类似的模式抽象成一个统一的理论框架。这个框架有助于我们在软件设计中确定求解算法的可复用组建。因为不需要对类似的细节进行多次重复编码，所以不仅编码的工作量降低了，编程错误也会减少。

一个算法必须回答几个问题：算法收敛性，算法是可停机的吗？算法正确性，结果是正确的吗？算法的复杂度可接受吗？

数据流分析的算法框架可以抽象为一个代数问题。数据流值全部可能的取值的幂集为V，在 V 上定义一个半格 (semi-lattice)，有meet 运算 ∧。两个元素的 ∧ 运算得到它们的最大下界。半格的 meet 运算 ∧ 有以下特点：

• 等幂：x ∧ x = x;
• 可交换 x ∧ y = y ∧ x;
• 有结合律x (y ∧ z) = (x ∧ y) ∧ z.

∧ 运算定义了半格上的偏序关系 ≤。半格的顶元素 T 满足：任意 x ∈ V, x ∧ T = x，底元素 ⊥ 满足：任意 x ∈ V, x ∧ ⊥ = ⊥。底即最小元素，顶即最大元素。

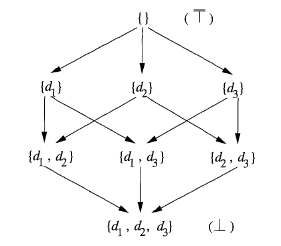
∧ 运算实际就是控制流约束。在控制流算法框架里面，就是并集或者交集运算，偏序关系实际就是包含或被包含关系。以定值问题举例，如图所示，所有可能的定值构成半格，顶为空集，底为满集。箭头的指向表明了偏序关系 ≤。控制流上的 meet 运算 ∧ 是并集运算∪, 偏序关系 ≤ 是 包含关系 ⊇。

框架中的传递函数族F: V → V，包含了块内的传递函数f，以及传递函数的组合。传递函数的组合封闭于函数族F。f ∈ F 是单调函数。x ≤ y 等价于 f(x) ≤ f(y).

基于以上模型，以正向传播为例，控制流算法框架的模型可以写作如下形式：

Init: 

    for each block:  Out[B] = T

Loop:

    In[B] = ∧ Out[P]   

    Out[B] = fb(In[B])

我们来看迭代过程。每次迭代，对每个程序点 p 上的值，In[B] = ∧ Out[P] 导致值在格上位置下降，fb(In[B]) 是单调函数也会导致值在格上下降。格的高度是有限的，基本块的数量也是有限的，所以迭代算法必然能够收敛。迭代得到的结果就是在格上组合传递函数的最大不动点。

从 Entry 到基本块 B 上的路径 p，所有经过的块的传递函数组合为 fp = f1▫f2▫f3…= f1(f2(f3…))), 最理想的解 IDEAL[B] = ∧ fp(Entry)，其中 p 为所有可能路径。IDEAL[B] 满足数据流方程组，而且根据单调函数 f ∈ F 的等价关系 f(x ∧ y) ≤ f(x) ∧ f(y) 知道，IDEAL[B] 是最大的正确答案，即精确解。迭代解是正确的，但是可能小于理想解，即不够精确。

因为迭代算法是格下降的，格的最大高度为值集中元素数量-1，以块为单位时，最大高度是块的数量-1。同时每次迭代需要遍历全部基本块，所以最恶劣情况下，时间复杂度为 O(n^2)，n 为基本块数量。

指针分析

指针分析也是静态分析的一个难点，对于一个指针，或者说是引用，我们能否在执行前或者说在编译阶段就知道他具体指向哪一块内存呢？基于这个特点我们可以做一些安全性分析与代码优化等等，但是知晓其指向的内存显然是不可以的，因为我们必须通过操作系统来分配内存从而得到确切的地址，但是在做静态程序分析的时候我们并不需要确切地知道他的虚拟地址或者物理地址是多少，只需要知道他在哪个堆，或者栈的哪个位置即可。遗憾的是可以通过证明发现我们也是不可以得到指针分析问题的确切解的，但是我们可得到可能解，来帮助我们完成指针分析。

因为指针本质上就是一个变量，改变指针的方法就是赋值，所以我们针对几种赋值语句来建立指针的联系，课程里讲到了两个指针分析的算法，分别是Andersen和Steensgaard算法。

Andersen算法

赋值语句	约束	意义	边
a = &b	$a\supseteq b$	$b \in pts(a)$	null
a = b	$a\supseteq b$	$pts(b) \subseteq pts(a)$	b -> a
a = *q	$q\supseteq *b$	$\forall v \in pts(q),pts(v) \subseteq pts(a)$	null
*p= b	$*p\supseteq b$	$\forall v \in pts(p),pts(b) \subseteq pts(v)$	null

表中的pts指的是point-to sets，即该指针变量可能指向的变量集合。例如a=&b,那么pts(a)表示a可能指向的变量集合，当然就可能包括b。同其他的数据流分析算法一样，Andersen算法本质上是一个简单通用的worklist算法，这里贴出伪代码：

举个例子：

int i, j, k;
int *a = &i;
           // a ⊇ {i}
int *b = &k;
           // a ⊇ {i}, b ⊇ {k}
a = &j;
           // a ⊇ {i, j}, b ⊇ {k}
int **p = &a;
           // a ⊇ {i, j}, b ⊇ {k}, p ⊇ {a}
int **q = &b;
           // a ⊇ {i, j}, b ⊇ {k}, p ⊇ {a}, q ⊇ {b}
p = q;
           // a ⊇ {i, j}, b ⊇ {k}, p ⊇ {a}, q ⊇ {b}, p ⊇ q
int *c = *q;
           // a ⊇ {i, j}, b ⊇ {k}, p ⊇ {a}, q ⊇ {b}, p ⊇ q, c ⊇ *q

对于上述代码，通过静态分析程序搜集约束信息之后可得一幅初始约束图。初始约束图的创建分为如下三步：

• 首先为程序中的每个变量建立一个节点
• 后根据基本约束标注节点的指向集
• 每一个初始的简单约束建立一条有向边

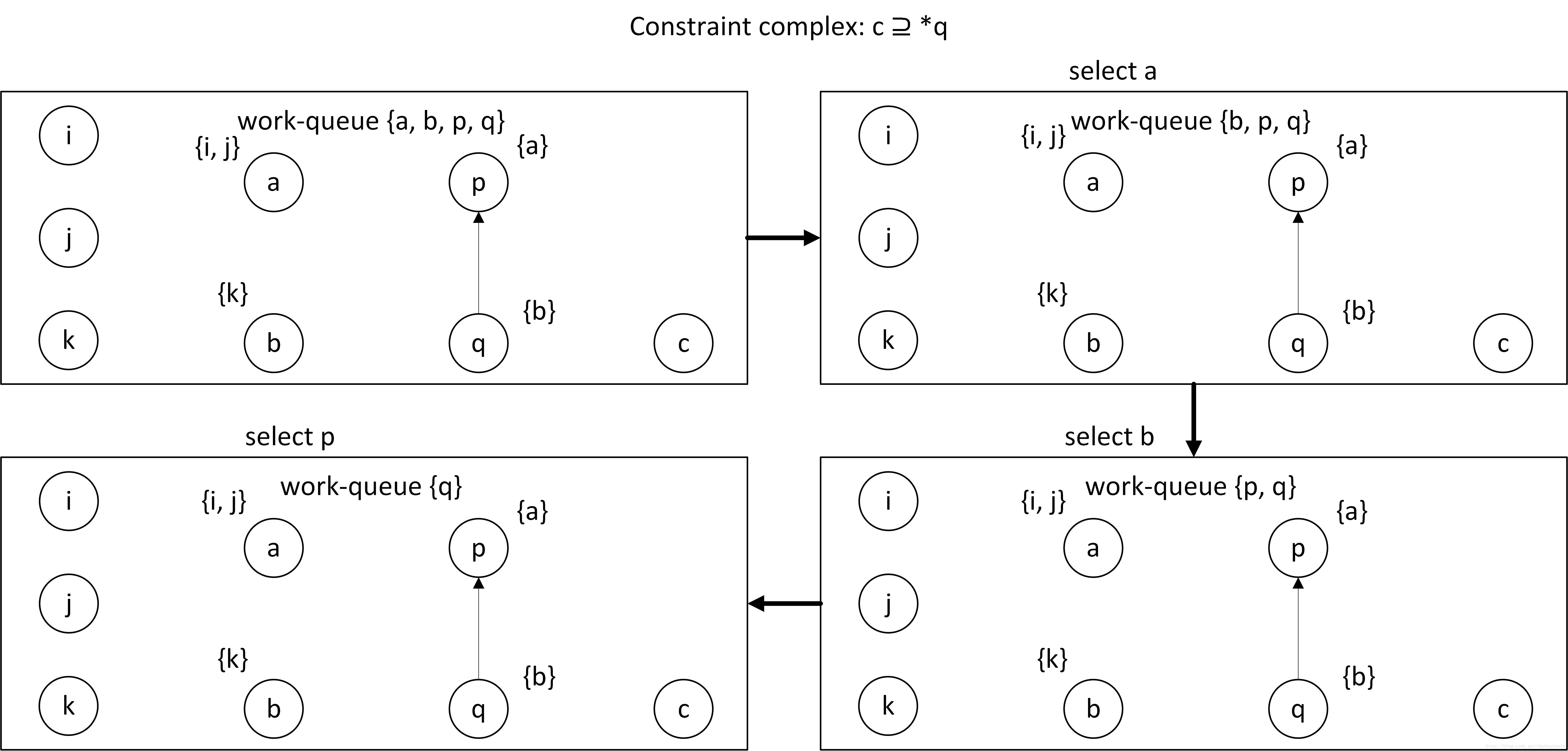
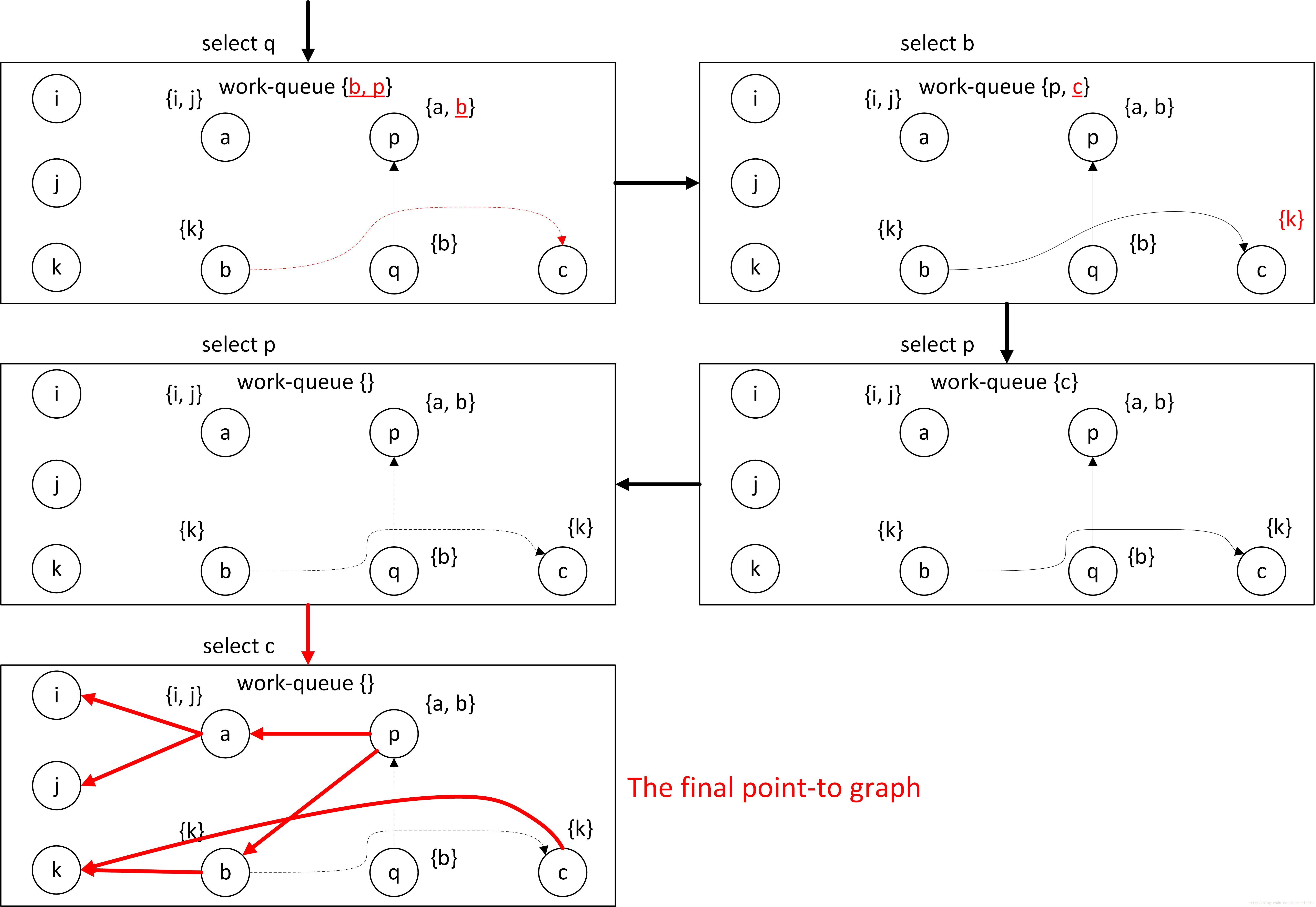
总而言之，我们首先根据简单约束条件完成初始约束图和worklist的创建，然后根据复杂约束遍历worklist来添加pts元素，最后得到所有可能的指针指向。

算法复杂度：N个结点，最多有O(N^2)条边。每条边被引入时最多引入O(N)连带反应(e.g. a->b->c->d…, abcd..依次入队列)，每条边最多引入一次, 所以复杂度是O(N^3)。

为了缩短时间复杂度，又有人提出了Steensgaard算法。

Steensgaard算法

显而易见，steensgaard缩短时间复杂度的手段是讲andersen算法中的subseteq符号都替换成了等号。

下面分析一下老师课件里的代码：

首先像Andersen算法一样，遍历swap函数之前的语句得到约束关系，画出约束图，然后分析swap函数，因为swap函数传入参数需要p=t1,q=t2得到，注意这里的等式含义是==，等式两边的内容是可以互换的：

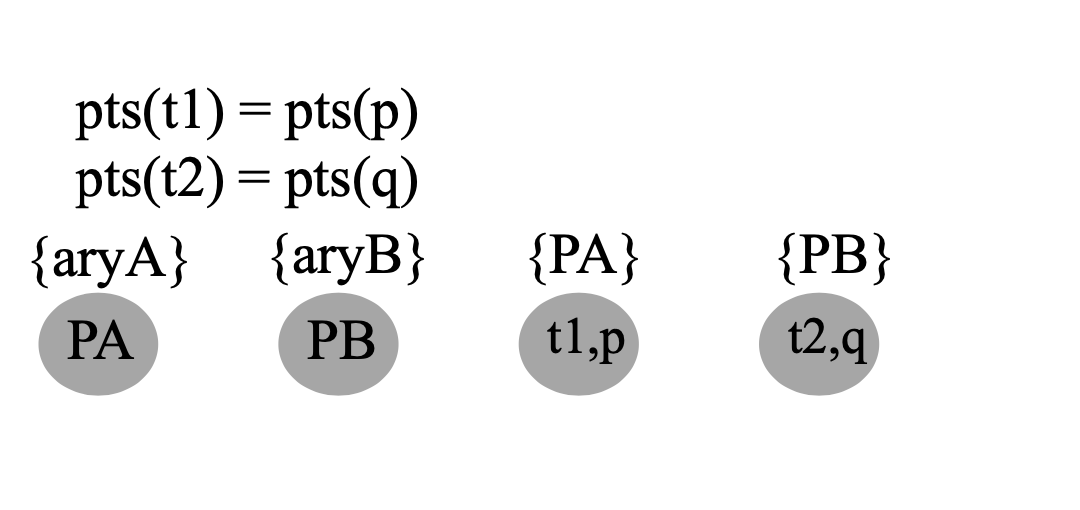
然后分析swap函数内的内容，最后得到：

这里的supseteq符号应该是等号。

总结

有关我作业的答案请看这个Github Repo等这学期考完所有的试再public吧（作业会有查重喔，而且助教老师们都是国内数一数二的程序分析团队，各种花里胡哨的查重手段不是问题..）如果你以后会从事编译相关的研究，或者说是沾上了一点边，比如我的话不是做程序分析的，是因为对tvm这些nn编译器比较感兴趣，还有可能会做的eda软件领域多多少少都会用好很多编译优化技术，那这门课会让你收获很多！如果老师们能够多腾出几节课，结合llvm的源代码来分析，把上课讲的算法实际写几个pass给我们debug一下就更好了，因为：板书实在看不清；而且看老师以及自己人工的模拟伪代码执行实在是太折磨了。