论文阅读｜Dual-side Sparse Tensor Core

A100卡（Ampere GPU Arch）上的Sparse Tensor Core的稀疏加速用的是类似FPGA19上的这篇《Efficient and Effective Sparse LSTM on FPGA with Bank-Balanced Sparsity》的Bank Sparsity的方法，硬件实现比较简单，而且有利于负载均衡。

简单来讲，在Sparse Tensor Core上，对于W*A，把大矩阵W拆分成很多个1*4的小块，然后强制让稀疏度为50%，即每4个元素，去除掉其中绝对值最小的两个值，这种稀疏压缩方式成为(2:4 bank sarsity)，对原本的tensor core也只需要做很小的修改，像下图中加一个mux四个有值的下标来选出与之匹配的矩阵A中的元素进行运算。

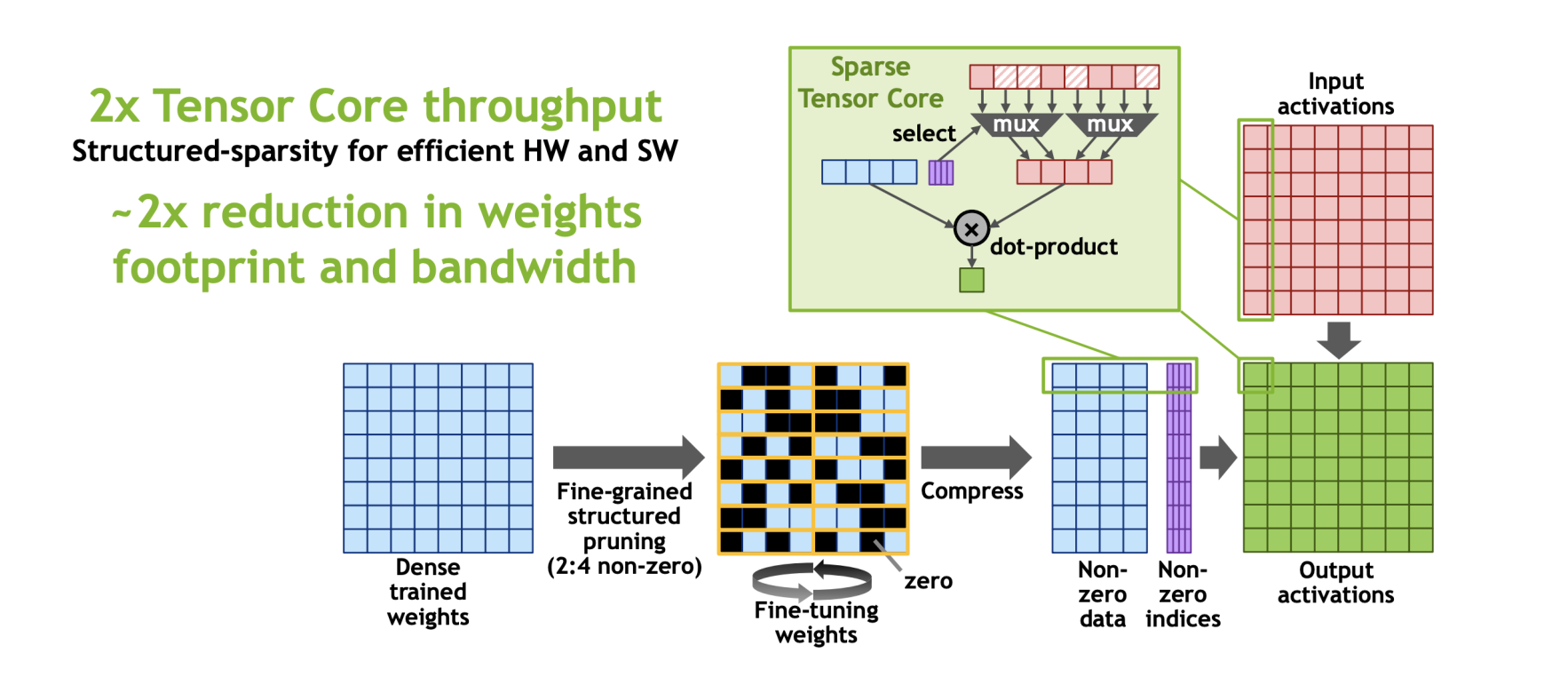
《Dual-side Sparse Tensor Core》指出这个sparse tensor core要求稀疏度是固定的50%，而且只考虑到了weight sparsity不能考虑到activation sparsity，于是魔改Sparse Tensor Core的一些工作(提出了一种新的、未探索的范例，它结合了 outer-product 计算原语和基于位图的编码格式)，在Accel-Sim（GPGPU的模拟器）上进行了验证。

inner-product vs outer-product

举例来讲，一个矩阵乘法C=A\*B,在C程序中可以这么写(图源：https://patterns.eecs.berkeley.edu/?page_id=158)：

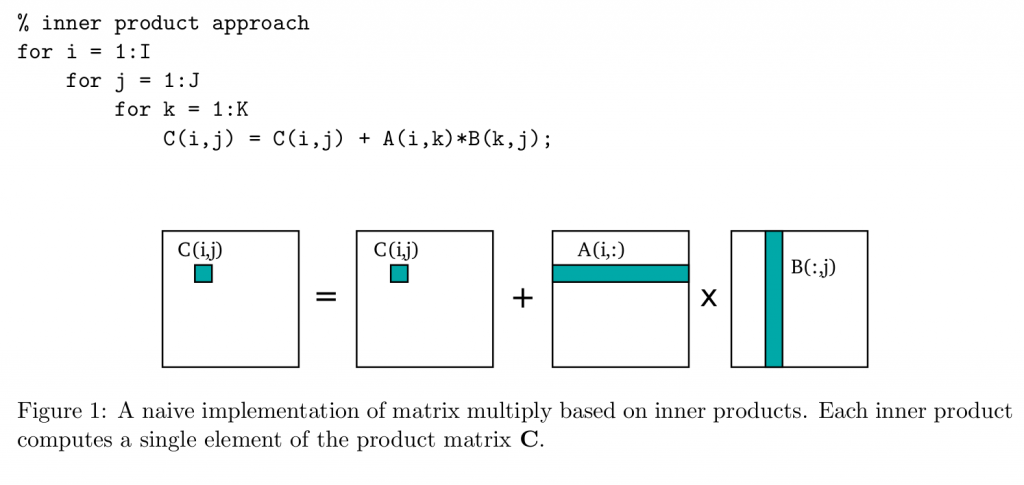
即取矩阵A的一行元素与矩阵B的一列元素进行点积，显然，对B(:,j)的访问会带来很大的访存开销，因为B(0,j)和B(1,j)很有可能不是在一个Cache Line里面。

outer product是指，将最内层的K循环提出到最外层：

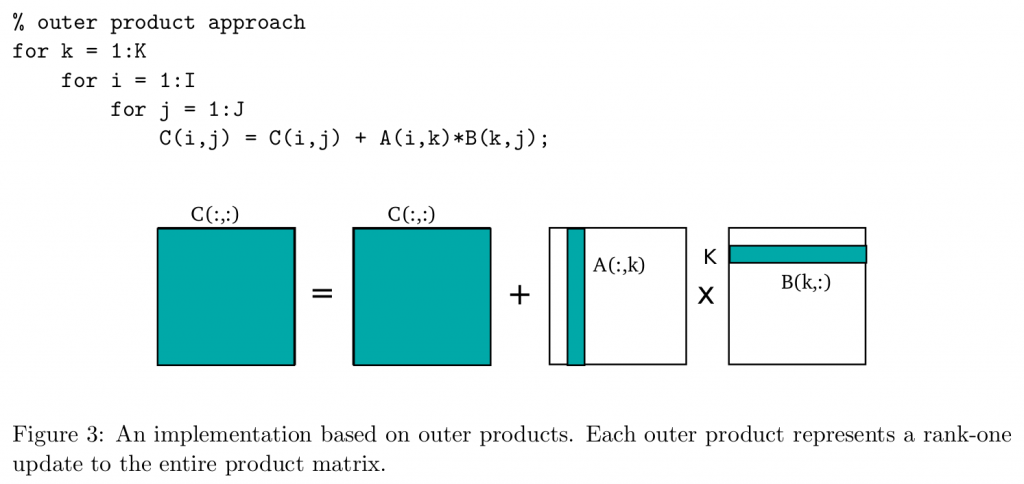
这样就变成了一个(m,1)的矩阵和一个(1,n)的矩阵相乘，得到k个(m,n)的矩阵相加。这种办法虽然不能缓解inner product不好的空间局部性的问题，但是这种形式非常适合来做矩阵分块：

分块的参数可以通过Auto Tuning的方式来寻找。

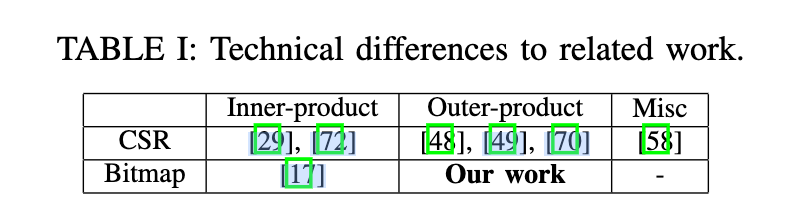
CSR vs Bitmap

两者都是一种稀疏矩阵的压缩方法，对于CSR来说：

CSR包含三个数组（所有的index从0开始）：

1. V，用来存储矩阵中的非零元素的值；
2. COL_INDEX，第i个元素记录了V[i]元素的列数；
3. ROW_INDEX, 第i个元素记录了前i-1行包含的非零元素的数量。

关于CSR的例子：https://zhuanlan.zhihu.com/p/342942385

Bitmap也称作位图算法：

优点：由于采用了Bit为单位来存储数据并建立映射关系来查找位置，因此可以大大减少存储空间，加快在大量数据中查询的时间。（有点哈希表的意思，但哈希中的value值数据类型可以丰富多样，而BitMap最终查到的value只能表示简单的几种状态。）

缺点：BitMap中的查询结果（value）能表达的状态有限，且所有的数据不能重复。即不可对重复的数据进行排序和查找。

实际收益

1.针对稀疏矩阵的位图压缩方法

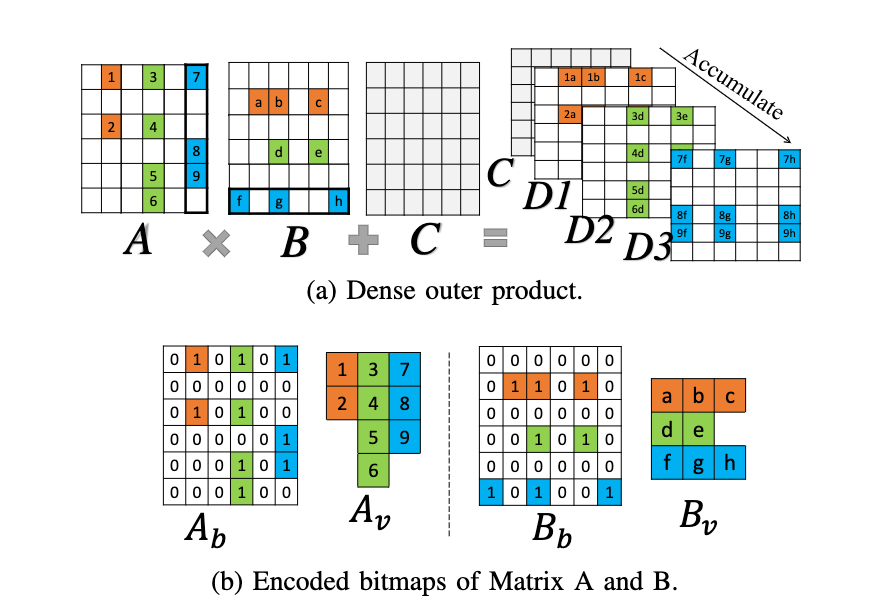
如图一个稀疏的矩阵，包括权重矩阵和特征矩阵都会被拆分成一个矩阵b(bitmap)和一个数值数组v(value)，如上图所示。

2.基于位图存储的outer product乘法

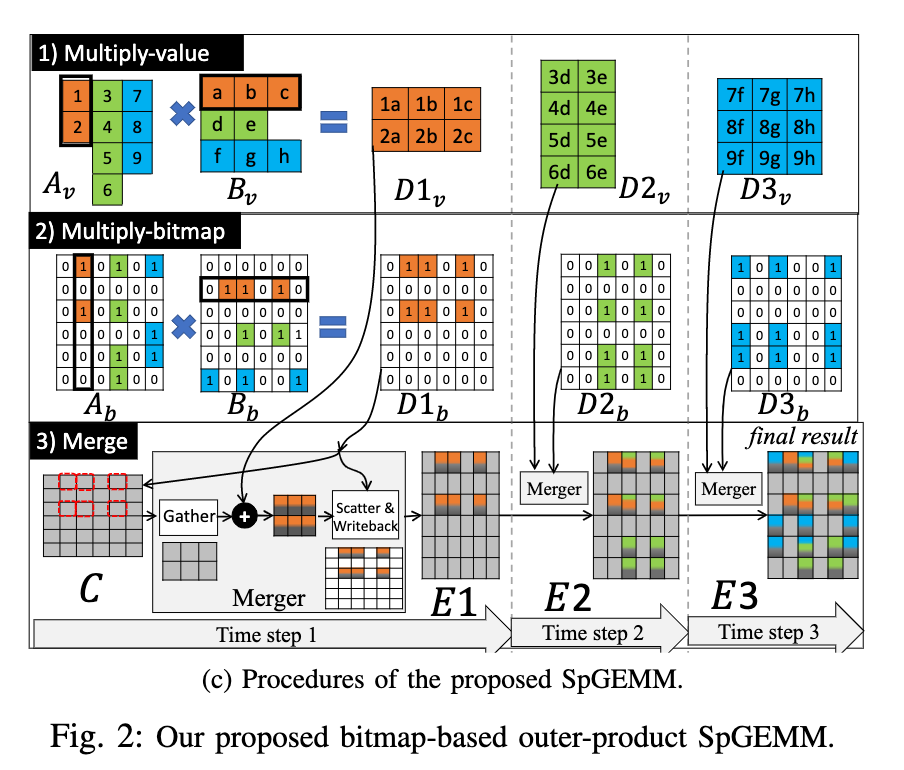
这个文章用的稀疏矩阵相乘的办法是，首先将v矩阵相乘，得到结果的值矩阵，然后再将bitmap矩阵相乘，得到结果的分布矩阵，最后进行一系列的Merger操作得到结果，Merger是先跟觉bitmap矩阵从输入的部分和矩阵中取得需要修改的数，再与值矩阵相加，最后再写回部分和矩阵，反复进行Merger操作得到最后的部分和。

3.魔改矩阵乘单元(Outer Product Tensor Core)

每个tensor core可以处理4*4*4大小的矩阵乘法，为了和tensor core的乘法器单元保持一致，这篇文章的阵列大小是8*8,(不过，为啥tensor core的矩阵乘大小是4*4*4的呢，因为考虑到了大扇出嘛？答案在：https://www.youtube.com/watch?v=Do_vEjd6gF0)

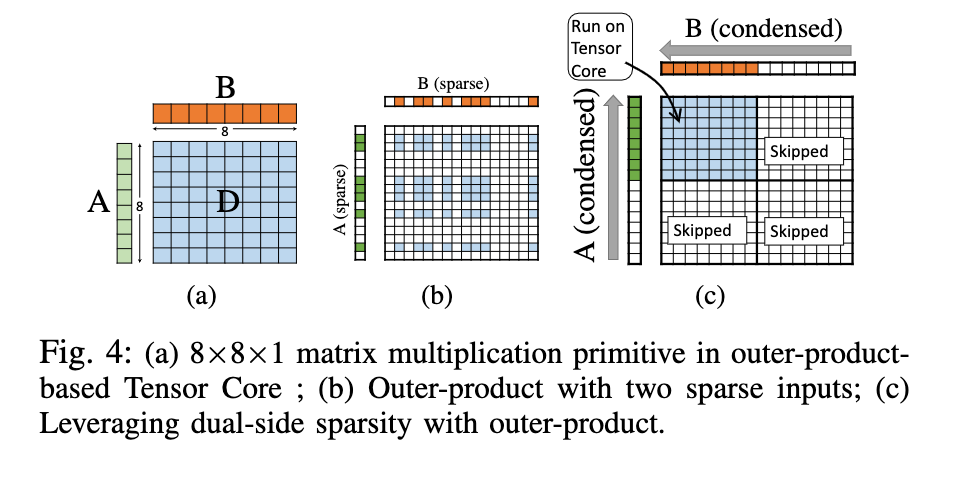
就是说，把A中的非零元素都塞到一起，B中非零元素都塞到一起，然后每8*8的矩阵进行运算得出部分和。（其实就是刚才的value矩阵outer product乘法的扩大版本，可能为了篇幅所以说了两遍？）

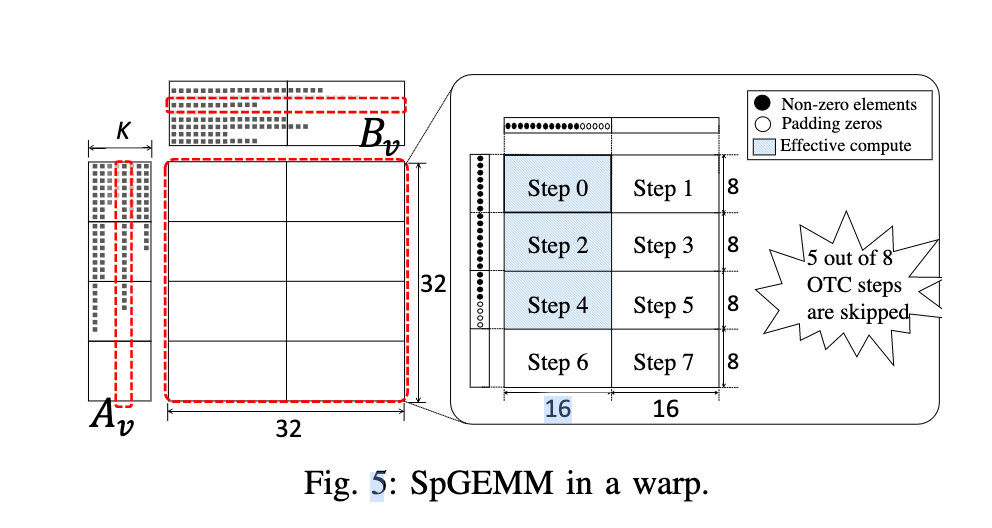
举个例子来讲，A和B的值矩阵大小分别为（32，k）和（k, 32），使用两个tensor core来做8乘16的矩阵运算，因为是outer-product的大小是（32，32）的，所以理论上我们需要做8次运算才能得到一个outer-product部分和矩阵（但是其实并不需要，如上图所示的某一个部分和矩阵，有五个tensor core的计算单元全都是0值，所以并不需要计算进而获得一部分的加速，这个加速比取决于A和B的稀疏度，对于如上图摆放的tensor core来说，A的稀疏度为<0.25,0.5,0.75,1>,B的稀疏度为<0.5,1>分别会来带固定的加速比。

Two-level bitmap encoding

如果矩阵过大，实际上中间矩阵确实非常大，那么bitmap矩阵就会变的很大，这个是bitmap经常存在的问题了，解决办法是做一个二级的bitmap。

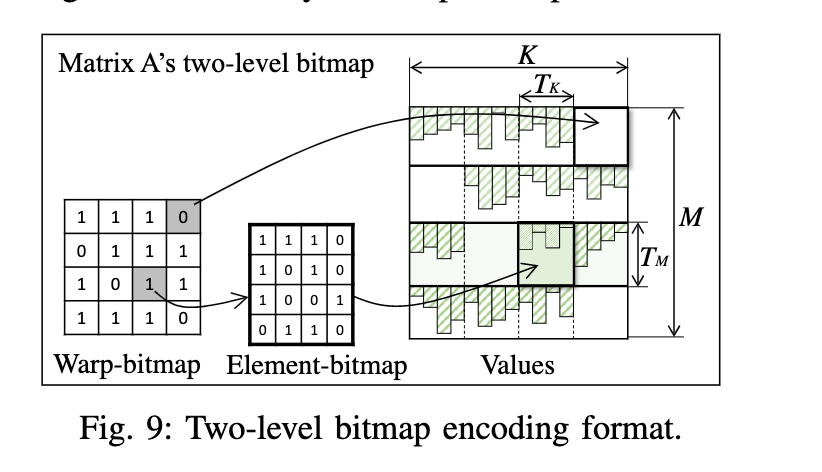
第一个warp bitmap表示tile是否有值，第二个Element-bitmap表示tile中非零元素存在的位置。

Outer-product friendly im2col

对于卷积运算，可以通过im2col的方法来转化成gemm计算，对于bitmap和value矩阵来说，也一样可以通过im2col的方法分别完成转换。

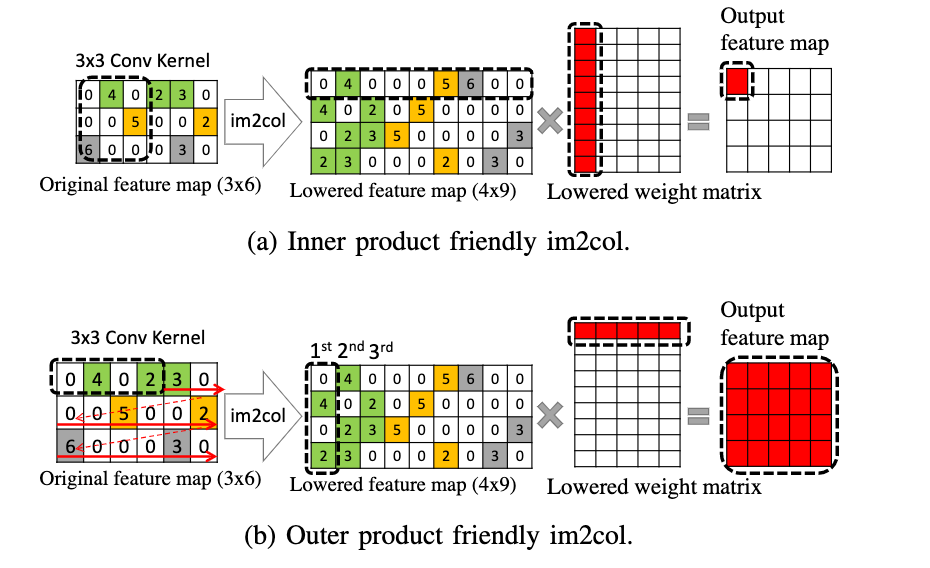
个人理解：因为A的im2col的结果矩阵的列元素在原始矩阵上是连续的（这样原本tensorcore隐式转换的方式访问的也是连续的内存），B的im2col结果在横向上是连续存储的，这样就可以完全利用空间局部性了。

其他

扩展了ISA来完成稀疏矩阵的运算，还有关于accumulation buffer的优化设计。

验证与结果

验证平台：基于Accel-Sim写的模拟器，对sparse Gemm来说大部分情况此文提出的架构都比sparse tensor core表现得要好（表里是运行时间，所以值越小越好）

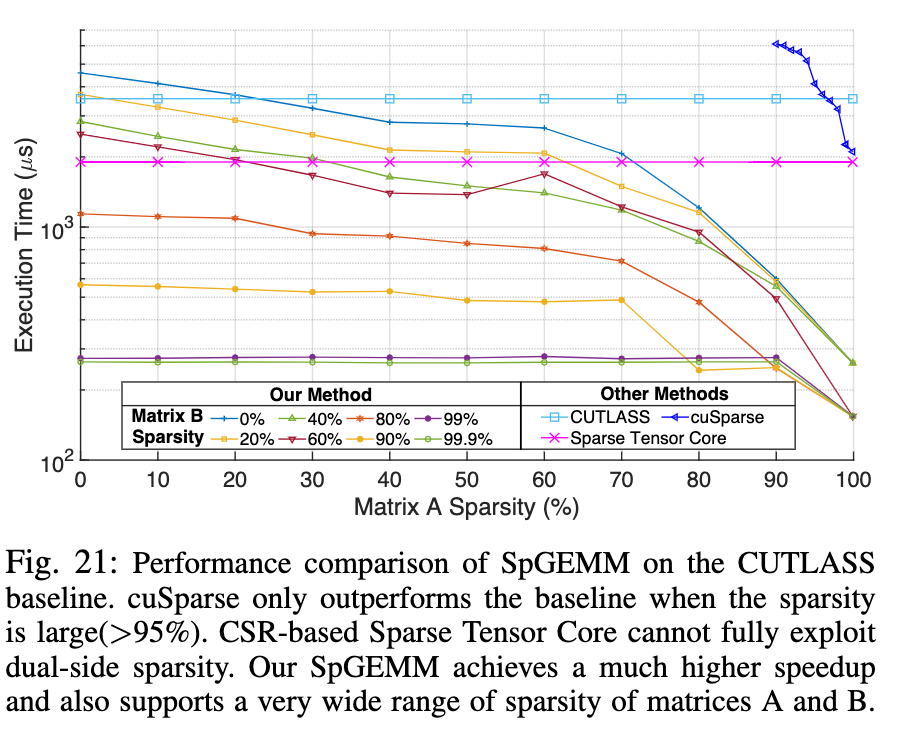
在稀疏网络的推理过程上也取得了不错的加速效果，面积仅仅大了2%

这篇文章在末尾说，证明了在GPU张量核上用(最小的硬件扩展?哪里有证明啊喂)实现SpGEMM和SpCONV有意义的加速比是可行的。本文最关键的insight是将矩阵乘法的outer-product方法和基于位图的稀疏编码相结合，实现高效的GEMM和 IMPLICIMT IM2COL 的双面稀疏，而硬件开销可以忽略不计。

但是经过这样魔改之后的sparse tensor core是不是会对dense gemm的性能有损失呢？

仍然不懂（待解决的问题：

1. However, performing the implicit im2col on the sparse input tensors is significantly more challenging than on the dense tensors because of the randomly distributed non-zero elements.In fact, we show that a naive implementation of implicit sparse im2col can be 10× to 100× slower than its dense version.

   为什么说sparse的隐式的im2col会比dense的慢一百倍呢？最差的情况下不应该是一样的吗？（来自谢师姐：了解了一下implicit im2col的实现（https://arxiv.org/abs/2110.03901）
   看起来是，通过初始memory的存放，搭配crossbar可以动态的读取lowered matrix
   在我看来，他说的naive implementation of implicit sparse im2col，可能是想把0计算跳过，把conv计算再展开成一个小的GEMM（？）
   但是这样的话，因为weight稀疏的不规则，就没办法按照dense的进行地址和crossbar的选择了，可能就会花的时间更久？（但是100倍，可能就得看他这个naive implementation具体是啥情况了吧））

2. 这个Global矩阵上带来的加速比，意思是全局的矩阵稀疏度虽然少于50%，但是仍然可以获得一定的加速比，我觉得这个是比较好理解的，只不过他给的这个图为什么是4个一分，按照他88的矩阵大小，不应该是8个元素分成一组吗？（我觉得应该是为了和原来的tensor core进行比较，所以进行了warp级别的对比吧，一个warp控制了两个tensor core来计算一个8\4的块。