大三上学期学的数字信号处理,Matlab 大实验可以自选题,想到老师上课说的 IIR、FIR 的区别,借助图像观察两种滤波器的区别。当然,现在大家使用的图像处理算法是现代滤波器,与经典滤波器分析问题的角度不同,但本质上还是对图像的滤波。本文为我基于 Matlab 语言实现的 IIR、FIR 滤波。
一、实验任务
\1. 利用 Matlab 实现简单的图像操作
\2. 为图像加上噪声,并用 Matlab 制作 FIR、IIR 带限滤波器,观察处理效果
\3. 利用 Simulink 搭建简单的图像处理工程
\4. 探究 Matlab 和 ModelSim 结合的 FPGA 图像处理仿真平台
二、主要实验仪器及材料
Windows 10 操作系统、Matlab2018a
三、基于 Matlab 的图像滤波
1.图像的读入
实验内容:
通过 Matlab 读入彩色图像,并获得其长,宽等基本信息。
实验步骤:
在 Matlab 工程目录下,保存一幅彩色图片,命名为image.jpg。
 )
)
使用 imread 函数可读入图像,并返回一个对象;使用 size 函数可返回函数的长宽信息;由于图像要通过滤波器,使用 rgb 三通道需要分别设计三种滤波器,为实验过程增加了不必要的工作量,所以本次实验处理灰色图像,使用 rgb2gray 函数可将 rgb 图像转化成灰度图。
%% 图像的读取以及转换
rawImg=imread(‘image.jpg’); %读取 jpg 图像
grayImg=rgb2gray(rawImg); %生成灰度图像
[row,col]=size(grayImg); %求图像长宽
生成的灰度图像如下图所示:
 )
)
2.添加噪声
实验内容:
为原图像添加噪声,为验证带限滤波器和非带限滤波器(中值滤波、卡尔曼
滤波)的特点、分别加入以下两类噪声。
1)多个单频率的正弦波噪声叠加。频率分别为:350Hz、400Hz、450Hz;
2)高斯白噪声;‘
实验步骤:
首先规定扫描频率和扫描时间间隔。再分别生成三种频率的正弦波,其长度需要与图像的像素点数匹配,并叠加成噪声:
fz1=350;fz2=400;fz3=450;% 三个噪声频率
noise=0.4sin(2pifz1n*T)+…
0.7sin(2pifz2n*T)+…
0.5sin(2pifz3n*T);% 噪声序列
为了将正弦波噪声叠加到图像上,首先需要将二维图像的数据作归一化处理,然后映射到一维。
normImgMartix=im2double(grayImg); % 图像数据进行归一化
rawMartix=zeros(1,row*col); % 初始化一维矩阵
for i=1:row
for j=1:col
rawMartix(col*(i-1)+j)=normImgMartix(i,j);
end
end %将 M*N 维矩阵变成 1 维矩阵
再进行灰度图像和噪声信号的叠加,并将一维变换到二维。
rawMartixWithNoise=rawMartix+noise;% 加入噪声的序列
noiseMartix=zeros(row,col);
% 一维变 M*N 矩阵
for i=1:row
for j=1:col
noiseMartix(i,j)=rawMartixWithNoise(col*(i-1)+j);
end
end
加入单频混叠干扰的图像如下图所示:
 )
)
再然后,再原始图像上加入高斯白噪声,Matlab 内置了噪声函数,调用语法如下。
whiteNoiseImg=imnoise(grayImg); % 加高斯噪声,给 simulink 用
加入高斯白噪声的图像如下图所示:
 )
)
3.设计数字滤波器
实验内容:
设计 IIR、FIR 数字低通滤波器。
低通滤波器性能指标,,
),
),
。
观察两种滤波器对加入了单频混叠噪声的图像的滤除效果,比较两者的优缺点。再观察两种低通滤波器对加入了高斯白噪声的图像的屡出效果,分析原因。
实验步骤:
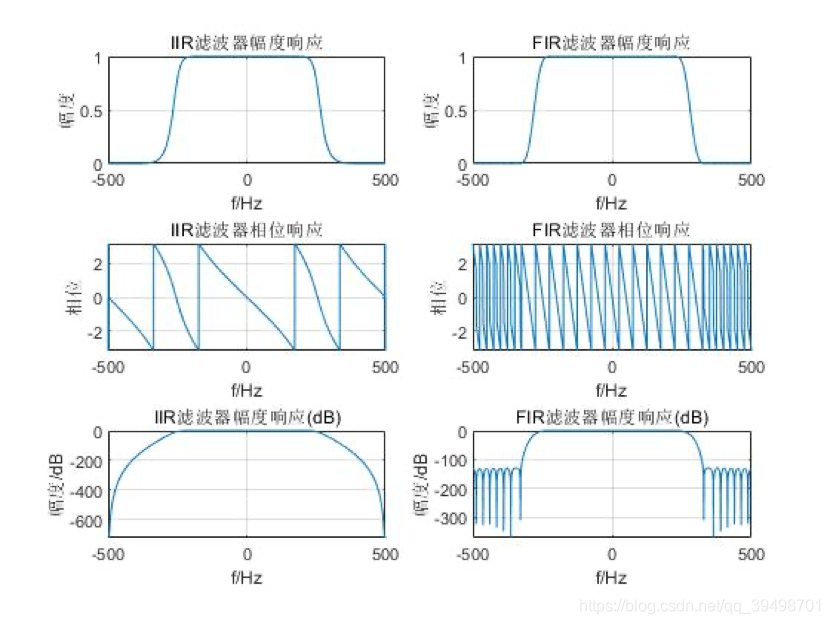
首先,设计 IIR 低通滤波器,用直接设计数字滤波器法设计巴特沃斯低通滤波器。再用 hamming 窗设计 FIR 低通滤波器,相关设计代码如下:
%% 设计 IIR 滤波器并分析相关指标
wp=2502/fs;ws=3002/fs;Rp=3;Rs=20;
[Nm,Wc]=buttord(wp,ws,Rp,Rs);
[b,a]=butter(Nm,Wc);
H=freqz(b,a,f2pi/fs);
mag=abs(H);pha=angle(H);
mag1=20*log((mag+eps)/max(mag));
%% 设计 FIR 滤波器并分析相关指标
wc=280*2/fs;
%6dB 截止频率 280kHz
fx=[0 wc wc 1];
m=[1 1 0 0];
%理想频幅响应
b1=fir2(40,fx,m,hamming(41));
H1=freqz(b1,1,f2pi/fs);
mag2=abs(H1);pha1=angle(H1);
mag3=20*log((mag2+eps)/max(mag2));
观察设计出的两种滤波器的特性。
 )
)
分别用 IIR、FIR 滤波器滤除图像中的单频混叠噪声,并且为了便于观察图像的频谱变化,做一次中心变换。
rawMartixWithNoiseWithIIR=filter(b,a,rawMartixWithNoise);
rawMartixWithNoiseWithIIRFFT=fft(rawMartixWithNoiseWithIIR);
rawMartixWithNoiseWithIIRFFTShift=fftshift(rawMartixWithNoiseWithIIRFFT);
其中,b,a 为设计出的滤波器的分子分母系数,将其带入为 IIR、FIR 滤波器相应系数即可。观察其滤除后的图像。
 )
)
对上述结果作简单分析:经过两个低通滤波器,高频干扰被滤除了。但是图像有部分失真,体现在图像的左边有小块黑点,这些黑点原本是属于图像的右侧。原因在于同一个像素点,经过滤波器会产生一定的延时,阶数越高,延时越大,由于相同指标下,FIR 的阶数比 IIR 的阶数要高,所以其产生的延时越大,效果也越差一点。但是由于 FIR 是线性相位,每一个点的延时都是相同的, 所以很好进行修正。下面探讨修正的方法。
4.对滤波后的图像进行相位修正
实验内容:
由于信号通过两类滤波器像素点会产生延时,会出现图像部分像素点偏移的
情况,现在探讨如何对这种情况进行修正。利用 Matlab 自带的 grpdelay 函数能够获得滤波器的延时情况。根据情况,给出解决方案。
实验步骤:
求解滤波器延时调用代码格式为:
grd=grpdelay(b,a,f2pi/fs);
上述代码中,b,a 为对应滤波器的分子分母系数。由于结果过于长,这里不列出。仅给出结论。对于 IIR 滤波器,不同的像素点输入后的群延时不同,对于 FIR 滤波器,每一个像素点的延时都是定值,在本实验中,该值为 20,所以我们只需要将 FIR 滤波器处理后的图像向前推移 20 位即可。编写代码如下:
K=round(mean(grd));
rawMartixWithNoiseWithFIRFixed=[rawMartixWithNoiseWithFIR((K+1):L),rawMartixWithNoiseWithFIR(1:K)];
再将图像转换成二维矩阵显示,处理后的结果如下图所示:
 )
)
但是对于 IIR 滤波器,由于延时不同,其失真不可挽回,且对于每个像素点都要减去相应的延时。即使能够勉强恢复图像,耗费的时间也是很大的。所以可以得出结论对于图像处理来说 FIR 滤波器比 IIR 滤波器更适合。
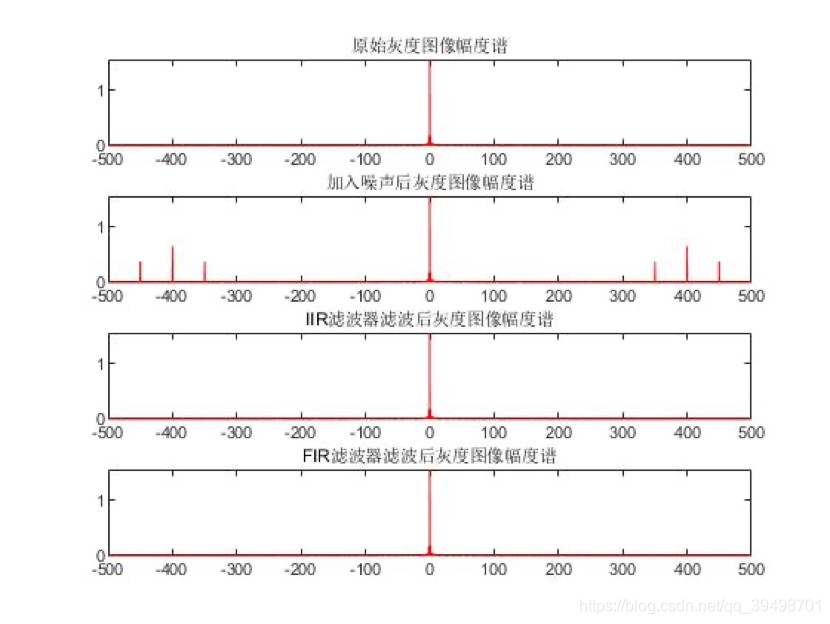
5.比较滤波前后图像的频谱
实验内容:
在一个窗口里画出图像经过 Matlab 处理过程中的频谱图,反应频谱变化。
实验步骤:
各状态的频谱图如下图所示:
 )
)
可以看到滤波器工作正常,各频率成分有被很好的滤除。调用 sound 函数回放声音,感受声音的变化。
5.高斯白噪声的滤除
实验内容:
对于高斯白噪声,首先尝试 FIR、IIR 滤波器的滤除方法,观察效果。后结
合 Simulink 给出更好的解决方案。
实验步骤:
首先,尝试用 IIR、FIR 滤波器对掺入噪声的图片进行滤波,效果如下图。
 )
)
可以发现,结果中看不到原始图像的特征。分析原因:高斯白噪声的频带覆盖了整个频谱,会将原始图像的频谱淹没。如果此时仍然使用带通滤波器很难再将原有的图像恢复。在网络上查阅资料不难发现,高斯白噪声较好的滤除方法是中值滤波。
中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术,中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替,让周围的像素值接近的真实值,从而消除孤立的噪声点。从其算法原理来看,对于上述人为添加的高频混叠干扰来说,中值滤波起不到很好效果,但对于高斯白噪声这一类随机噪声,能够起到较好的过滤作用。
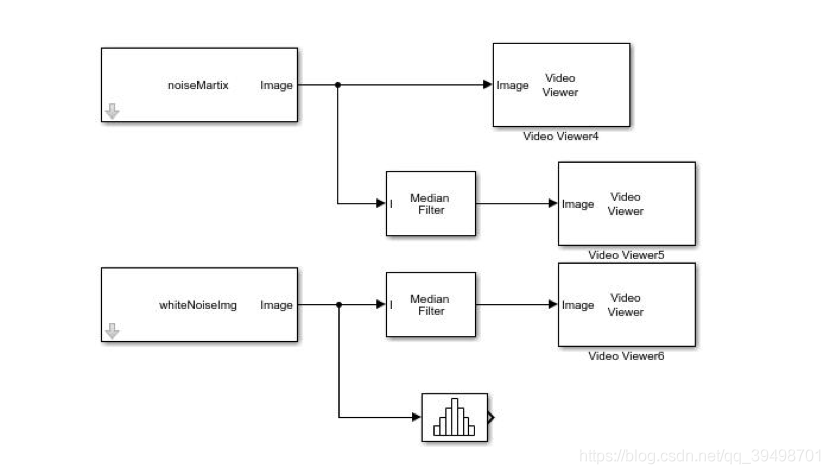
接下来,在 SimuLink 里搭建图像处理平台与中值滤波环境。简单介绍一下使用到的模块:
Image From Workspace: 获取工作区的图像类型,获取白噪声。
Median Filter:中值滤波。
Video Viewer:能够将图像矩阵可视化显示的模块。
在 SimuLink 中搭建工程如下图所示:
 )
)
运行后,结果如下图所示:
 )
)
可见,相对于带限滤波器而言,中值滤波对白噪声的处理有更好的效果。
Comments