Write High Performance Matrix Multiplication via TileLang

在Tile Language目前的设计理念中，我们提供了三种不同的编程接口，分别面向初学者、开发者和写Kernel的专家这三个等级，我们对Level 1的使用者的定义是不清楚目标硬件架构的开发者（例如不知道GPU的cache一般需要用到tiling，把数据层层cache），这个时候用户编写的程序只是一个简单的计算表达式，不包含任何schedule相关的信息（和tvm的设计一样），这种方法理论上来讲对于不太kernel的人是最舒服的，但是因为很多现存未解决的问题：

1. 从调优的角度来看，从计算到具体的schedule的自动调优时间一般要花比较久的时间，虽然一些工作例如MSRA System Research的Roller，利用硬件感知的白盒搜索空间生成缓解了这一问题, 请看BitBLAS对Roller的复现[Tutorial](https://github.com/microsoft/BitBLAS/blob/main/tutorials/1.fast_and_efficient_codegen.ipynb), 但知道并使用这种方法的人的人也不是很多
1. 从Kernel的表达能力角度来看，目前一些主流的复杂的计算并不能够通过schedule描述出来，例如Flash Attention, 虽然理想上应该可以通过推导 matmul+softmax+matmul 简单计算表达式的一种算子融合版本得到，但是这个问题从写文章的时间点来看仍然很困难。
1. 从社区来看，Schedule的代码虽然看起来还是很优雅的（从写schedule和理解schedule的角度来看, 例如bitblas对于matmul dequantize的[schedule模版](https://github.com/microsoft/BitBLAS/blob/main/bitblas/gpu/matmul_mma_dequantize.py)我个人觉得还是写的很通用的)，schedule的魅力在于其从一个最原始不包含任何调度信息的计算表达式，在确保正确性不受影响的情况下一步步变换到最终的高性能调度形式。但是schedule实在太难学习和理解了，即使是一个会写schedule表达式的开发者（这部分玩家已经很少了），想要看明白我写的各种schedule模版，继续扩展也是非常非常困难的。其次，很复杂的计算，例如Flash Attention, 其因为设计本身是要在shared memory上进行算子融合所以计算是无法表达的，其次，即使是要强行写出特别针对Flash attention的多算子fuse版本的schedule模版，schedule本身的代码量可能会比cuda还要长(最后，同样受限于社区，tvm的生态逐渐变得不如triton，一些新feature例如tma这些的支持会有点滞后)

于是在搞bitblas的时候我就觉得这一套有点难受(, 于是觉得需要一个类似triton的东西，但是triton的限制也很大，例如不能显式声明内存，不能显式控制线程的行为等，这一点之后分享的时候再讨论讨论。总之目前bitblas的所有kernel实现都已经换成了Tile Lang，自己用起来非常舒服。

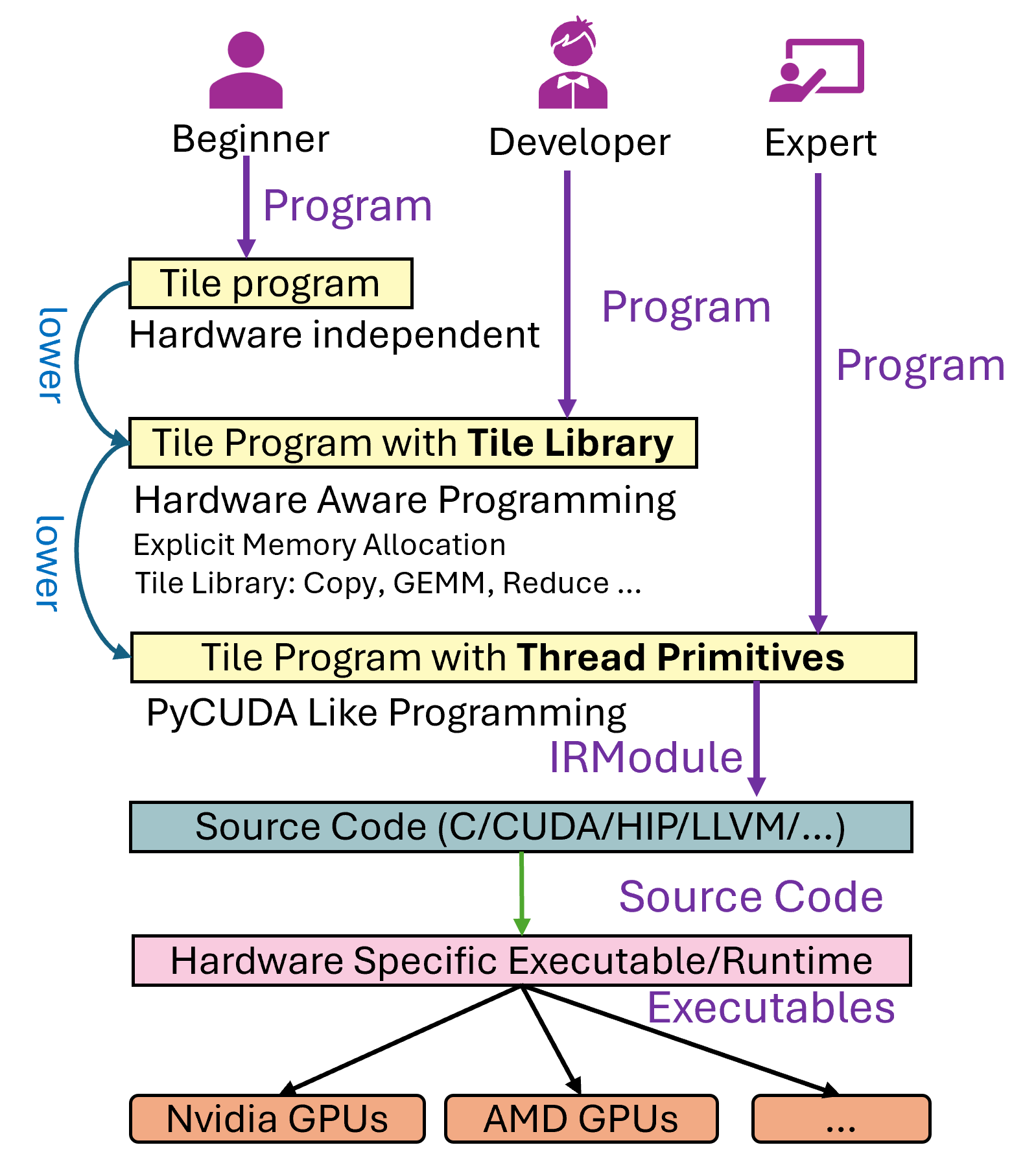
话说回来，我们对Level 2的使用者的定义是知道目标硬件架构的开发者，及在cuda上知道shared memory这个概念，知道在cuda上做tile要先把数据load到一个高速的缓存上再进行计算（有点类似triton的开发模式），本文我们以这种模式为例子介绍一下矩阵乘法Kernel的组成。

最后提一嘴Level 3, thread primitives允许用户完全控制每个线程的行为，写这一部分的代码其实就和写PyCUDA差不多了(但是支持多后端，例如HIP等)，于是Level 3就是给完全的expert写的了，但本质上，经过LowerTileOP和LayoutInference这两个Pass之后，Level 2的代码也会被Lower到Level 3上。

所以非常值得一提的是，我们的设计中这三种语法可以出现在同一个program中，例如BitBLAS里的量化矩阵乘法的program中对于复杂的反量化部分，我们使用了thread primitives来精心控制每个线程的行为，以及利用ptx来加速精度转换的过程，显式在progam中调用mma 来在一些情况下在寄存器中做反量化等，其他的一些操作，例如数据拷贝和Pipeline仍然使用Level 2的编程方式(T.Pipelined, T.Copy)等，代码参考matmul_dequantize_tensorcore_finegrained.py。

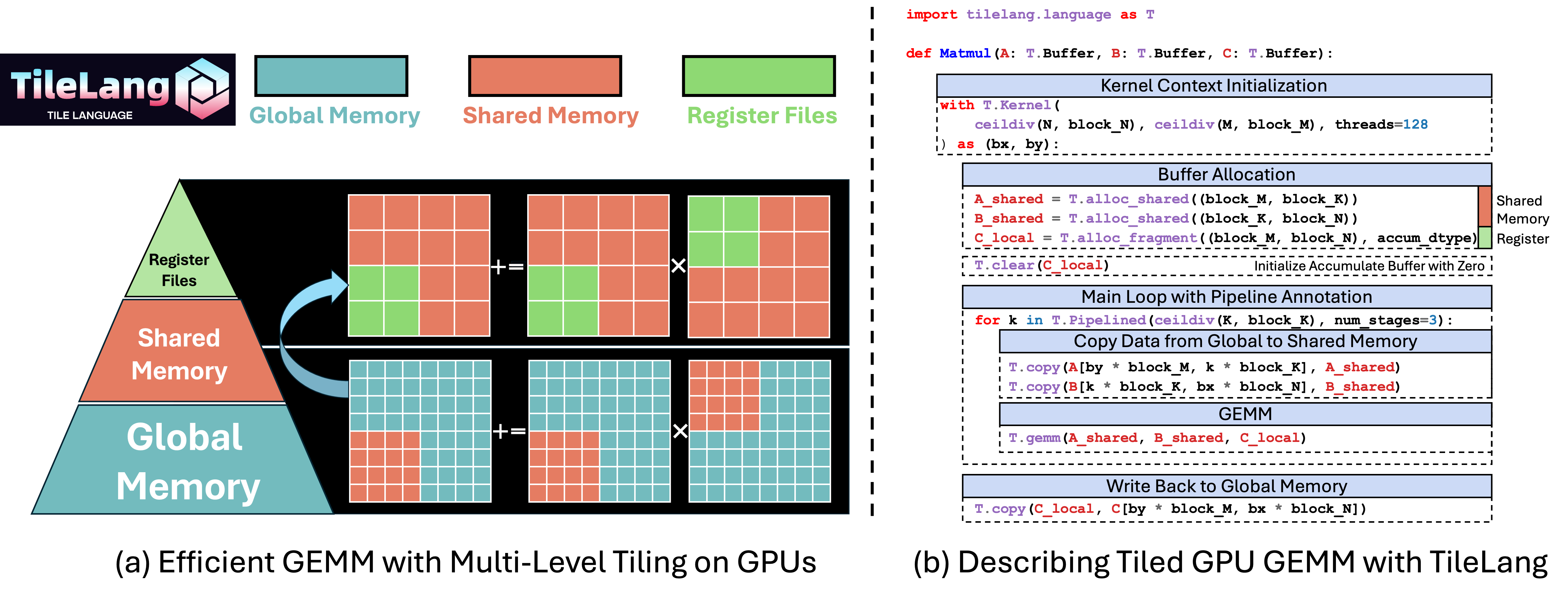
一个Level 2的矩阵乘法的Kernel如下(提前兜底，同样的Code加上auto tune，在A100/H100/MI300X上性能都和vendor comparabel, MI300上略好).

import tilelang
import tilelang.language as T
# `make_mma_swizzle_layout` is a python defined layout function
# specifically designed for for MMA operations
# which ensures the consistency with the nvidia CUTLASS Library.
# to avoid bank conflicts and maximize the performance.
from tilelang.intrinsics import (
    make_mma_swizzle_layout as make_swizzle_layout,)

def matmul(M, N, K, block_M, block_N, block_K, dtype="float16", accum_dtype="float"):
    # add decorator @tilelang.jit if you want to return a torch function
    @T.prim_func
    def main(
        A: T.Buffer((M, K), dtype),
        B: T.Buffer((K, N), dtype),
        C: T.Buffer((M, N), dtype),
    ):
        # Initialize Kernel Context
        with T.Kernel(T.ceildiv(N, block_N), T.ceildiv(M, block_M), threads=128) as (bx, by):
            A_shared = T.alloc_shared((block_M, block_K), dtype)
            B_shared = T.alloc_shared((block_K, block_N), dtype)
            C_local  = T.alloc_fragment((block_M, block_N), accum_dtype)

            # Apply layout optimizations or define your own layout (Optional)
            # If not specified, we will deduce the layout automatically
            # T.annotate_layout({
            #     A_shared: make_swizzle_layout(A_shared),
            #     B_shared: make_swizzle_layout(B_shared),
            # })

            # Enable rasterization for better L2 cache locality (Optional)
            # T.use_swizzle(panel_size=10, enable=True)

            # Clear local accumulation
            T.clear(C_local)

            for ko in T.Pipelined(T.ceildiv(K, block_K), num_stages=3):
                # Copy tile of A
                # This is a sugar syntax for parallelized copy
                T.copy(A[by * block_M, ko * block_K], A_shared)

                # Demonstrate parallelized copy from global to shared for B
                for k, j in T.Parallel(block_K, block_N):
                    B_shared[k, j] = B[ko * block_K + k, bx * block_N + j]

                # Perform a tile-level GEMM on the shared buffers
                # Currently we dispatch to the cute/hip on Nvidia/AMD GPUs
                T.gemm(A_shared, B_shared, C_local)

            # Copy result back to global memory
            T.copy(C_local, C[by * block_M, bx * block_N])

    return main


# 1. Define the kernel (matmul) with the desired dimensions
func = matmul(1024, 1024, 1024, 128, 128, 32)

# 2. Compile the kernel into a torch function
# out_idx specifies the index of the output buffer in the argument list
# if out_idx is specified, the tensor will be created during runtime
# target currently can be "cuda" or "hip" or "cpu".
jit_kernel = tilelang.JITKernel(func, out_idx=[2], target="cuda")

# 3. Test the kernel in Python with PyTorch data
import torch

# Create random input tensors on the GPU
a = torch.randn(1024, 1024, device="cuda", dtype=torch.float16)
b = torch.randn(1024, 1024, device="cuda", dtype=torch.float16)


# Run the kernel through the JIT-compiled function
c = jit_kernel(a, b)

# Reference multiplication using PyTorch
ref_c = a @ b

# Validate correctness
torch.testing.assert_close(c, ref_c, rtol=1e-2, atol=1e-2)
print("Kernel output matches PyTorch reference.")

# 4. Retrieve and inspect the generated CUDA source (optional)
cuda_source = jit_kernel.get_kernel_source()
print("Generated CUDA kernel:\n", cuda_source)

# 5.Pofile latency with the profiler
profiler = jit_kernel.get_profiler()

latency = profiler.do_bench()

print(f"Latency: {latency} ms")

下面来分析一下这个测试代码的主要组成：

1.使用 T.Kernel来初始化上下文

with T.Kernel(T.ceildiv(N, block_N), T.ceildiv(M, block_M), threads=128) as (bx, by):
    ...

• bx，by 分别表示线程块在 N 和 M 方向的网格方向的索引，也就是会自动帮你bind到BlockIdx.x和BlockIdx.y上，但其实这一步相当于一个语法糖，在Kernel内部写上

  for bx in T.thread_binding(N // block_N, "blockIdx.x")

  效果是一样的。

• threads=128是一个比较关键的上下文初始化，其指定了一个 block 中启动 128 个线程，这将被用来自动推导线程的映射(例如将T.Parallel Lower 到Thread Primitives)，也可以在后续用更低级的语法（Level 3）里做更精细的控制，通过tid = T.get_thread_binding()那到对应每个线程的迭代器。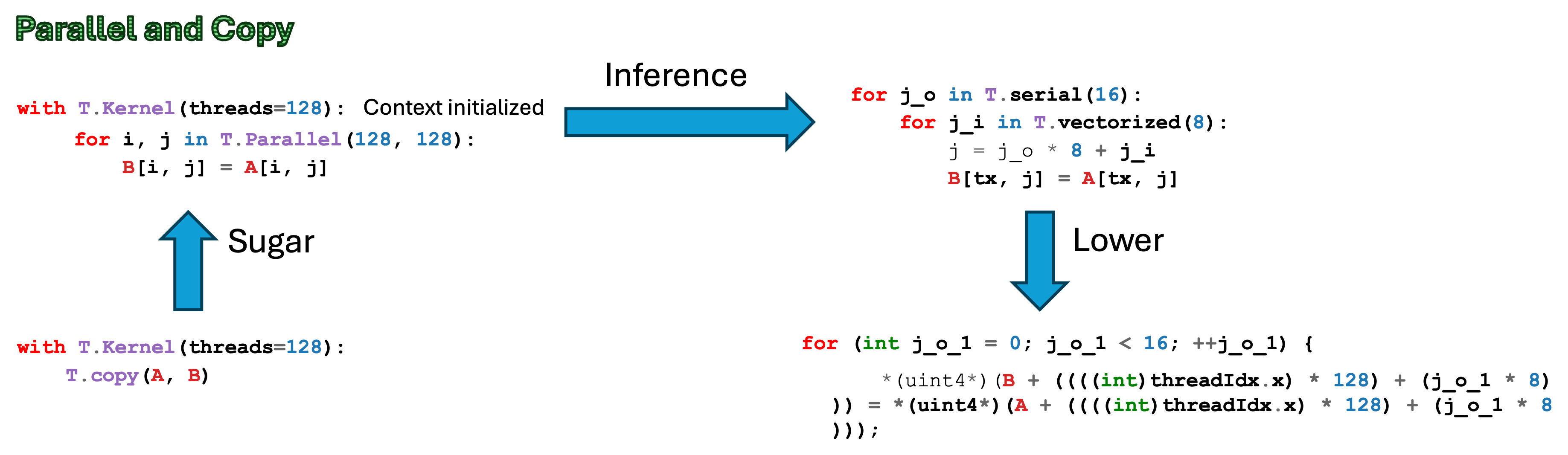

  

2. 显式分配Block级别的Shared Memory / Register Files

A_shared = T.alloc_shared((block_M, block_K), dtype)
B_shared = T.alloc_shared((block_K, block_N), dtype)
C_local  = T.alloc_fragment((block_M, block_N), accum_dtype)

• T.alloc_shared 表示分配 GPU Shared Memory，用于缓存当前tile对应的 A、B 子矩阵数据(此处默认使用dynamic shared memory, 如果要用静态shared memory, 可以将写作 T.alloc_shared((block_M, block_K), dtype, scope="shared"), 默认的scope为shared.dyn)
• T.alloc_fragment 与之相似，但这里分配的是本地寄存器空间，用来放累加结果，但是gpu上shared memory由整个block共享，寄存器文件确实每个线程独有的，为什么这两个的shape是一样的呢？这是我们的机制用来降低用户的心智负担，我们会有layout inference pass来自动推导出每个线程hold的寄存器文件映射。

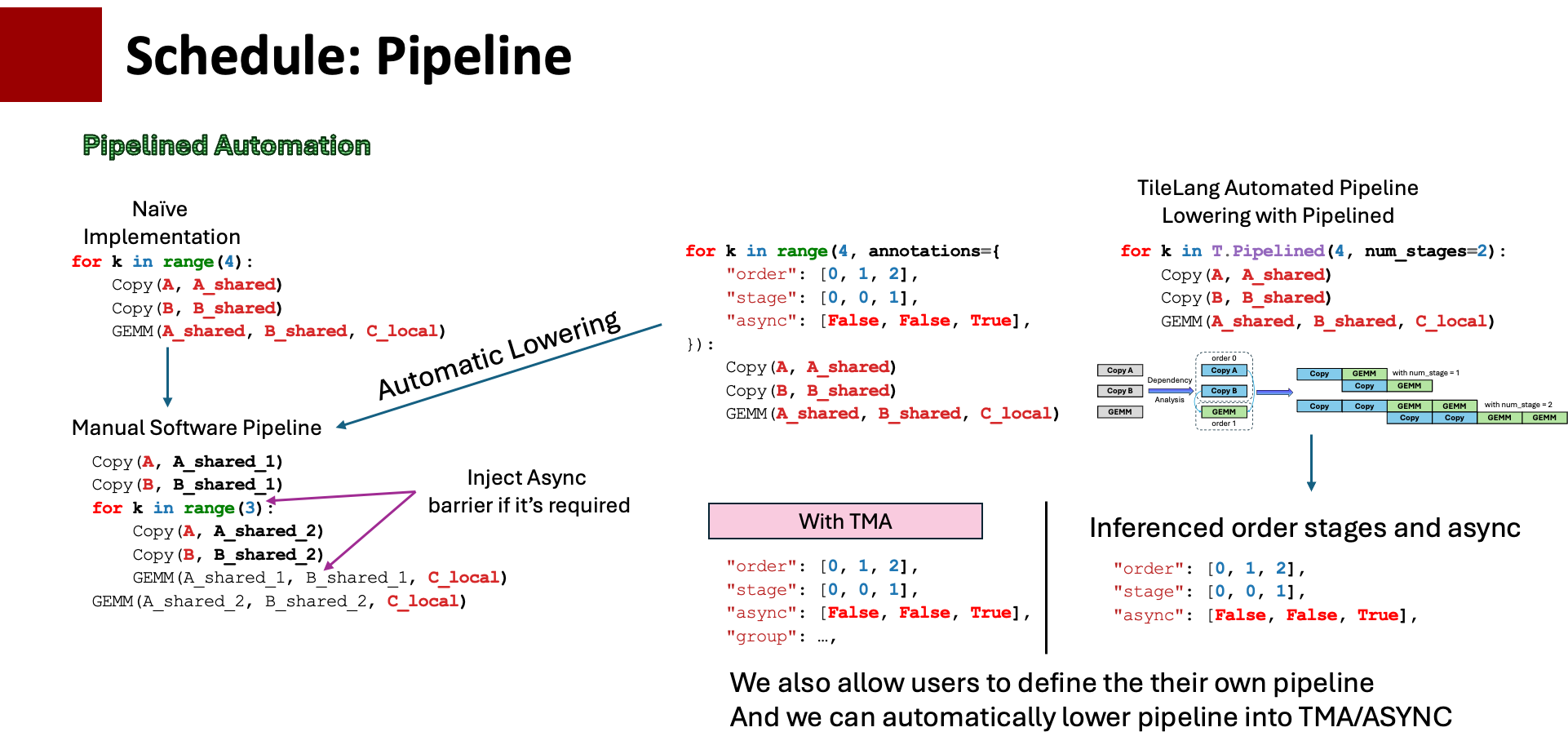
3. T.Pipelined自动软件流水

如下图所示，最直接的软件流水实现就是用户自己将k层for loop做流水实现，讲将一个for循环的copy部分拉出，最后一个循环的矩阵乘法部分拉出，这里的难点是需要自己分析出依赖和数据索引。

在tvm里面已经有一些关于pipeline的自动化方法，用户对一个循环进行一些标记，例如 order, stage, 软件就可以自动根据这些标记进行pipeline展开，但是这么做一方面不能保证正确性，另一方面用户写这个东西的心智负担也很大。

在这里，我们引入了T.Pipelined ，一个更高级的软件流水封装，用户只需要给一个stage(例如stage=2的时候就是double buffer), 我们会对代码块的Buffer使用进行一个依赖分析，自动推导出pipeline的各种属性，其次，包括异步拷贝，H100上的TMA等都隐藏在了Pass里，当然在stage2的时候，pipeline可能会有很多种组合，如果用户想自己定制Pipeline，也可以手动设置这些参数 。

for ko in T.Pipelined(T.ceildiv(K, block_K), num_stages=3):
    ...

4. Parallel自动并行化

T.Pipelined内部是循环的主体，其主要做内存拷贝和乘累加计算:

1. T.copy(A[by * block_M, ko * block_K], A_shared)

   这是一个T.Parallel的语法糖。我们只需要告诉编译器源和目的的起始地址，编译器就会按照 A_shared 的形状自动生成并行的加载指令。

2. for k, j in T.Parallel(block_K, block_N):
       B_shared[k, j] = B[ko * block_K + k, bx * block_N + j]
      这里用 `T.Parallel` 指明了 `k, j` 的循环可以并行执行。编译器也会根据线程数自动做映射，尽量生成高效的并行加载。
   
   3. T.Parallel不只可以被用到数据拷贝，例如乘累加的并行化操作都可以使用T.Parallel来操作。
   
   #### 5. `T.gemm(A_shared, B_shared, C_local)`
   
   `T.gemm` 是对“tile 级别矩阵乘法”的一个 调用。根据后端 target 的不同，它可能会被映射到：
   
   - NVIDIA GPU 上使用cute，在A100上用mma，H100上用WMMA。
   - AMD GPU 上本来使用的是composable kernel（但是封装的实在有点难搞，现在是我们自己用hip封装的。
   
   我们也可以通过tilelang 自举出这一个tile级别的矩阵乘，详见https://github.com/tile-ai/tilelang/blob/main/testing/python/kernel/test_tilelang_kernel_gemm_mma_intrinsic.py
   
   ```python
   for ko in T.Pipelined((K // block_K), num_stages=stage):
     # Load A into shared memory
     for i, k in T.Parallel(block_M, block_K):
         A_shared[i, k] = A[by * block_M + i, ko * block_K + k]
   
     # Load B into shared memory
     for j, k in T.Parallel(block_N, block_K):
         B_shared[j, k] = B[bx * block_N + j, ko * block_K + k]
   
     for ki in T.serial(0, (block_K // micro_size_k)):
   
         # Load A into fragment
         mma_emitter.ldmatrix_a(
             A_local,
             A_shared,
             ki,
         )
   
         # Load B into fragment
         mma_emitter.ldmatrix_b(
             B_local,
             B_shared,
             ki,
         )
   
         # Perform Matrix Multiplication
         mma_emitter.mma(A_local, B_local, C_local)
   

将原本的T.gemm展开成tilelang自己的ldmatrix和mma的实现，让你更细粒度的控制代码。

cuda上的gemm支持四种类型的输入:ssr, rsr,srr,rrr,其中s代表shared memory, r代表寄存器，例如:

T.copy(A[by * block_M, ko * block_K], A_shared)
T.copy(A_shared, A_local)
T.gemm(A_local, B_shared, C_local)

此时的gemm使用的就是rsr, 这样允许我们清楚哪部分的tile data可以在寄存器上复用（例如flash attention,

此外，gemm还有一些额外的参数:

• k_pack: 用作AMD上的Matrix Core优化，将k_pack个mfma指令拼接成一个大mfma，这个非常巧妙
• policy: 决定了n个warp共同计算的gemm应该怎么卸载任务，例如fullrow就是按行铺，fullcol就是按列铺等
• transpose_a, transpose_b: 这个两个输入是否是transpose的

最后一步 T.copy(C_local, C[by * block_M, bx * block_N]) 用于把 C_local 中的累加结果回写到 global memory。

---

即时编译部分

在示例里，我们把上述的 main 函数通过 matmul 这个 Python 包装函数返回：

func = matmul(1024, 1024, 1024, 128, 128, 32)

并调用 tilelang.JITKernel(func, out_idx=[2], target="cuda") 把它编译成可直接调用的 PyTorch 函数：

jit_kernel = tilelang.JITKernel(func, out_idx=[2], target="cuda")

• out_idx=[2] 告诉jit，函数形参中第 3 个 buffer (C) 是输出，需要在运行时自动分配一个 Tensor 给它。
• target="cuda" 则指定了要在 NVIDIA GPU 上编译和运行，目前支持cuda, hip, c for cpu.

接下来就是常规的 PyTorch 端到端测试了，生成输入 a, b 并调用 jit_kernel(a, b)，最终获得输出 c 并与 PyTorch 自带的 a @ b 做误差对比。

torch.testing.assert_close(c, ref_c, rtol=1e-2, atol=1e-2)
print("Kernel output matches PyTorch reference.")

如果一切正常，我们就能看到 “Kernel output matches PyTorch reference.” 的提示。

当我们调用 jit_kernel.get_kernel_source() 时，就能打印出编译器为这段 Tile Lang 代码生成的最终 CUDA 源码。通常里面会有很多注释和展开后的线程并行逻辑，对需要做底层调优的用户和调试来说非常有帮助。

我们用

profiler = jit_kernel.get_profiler()
latency = profiler.do_bench()
print(f"Latency: {latency} ms")

来测一下这个 Kernel 在实际硬件上的latency表现，可以快速验证一下自己写的kernel性能是否达到了预期。

最后分享一下在各个设备上关于矩阵乘法的性能（当然这里需要使用autotune tune一把，这也是一个有意思的问题，之后可以再讨论）:

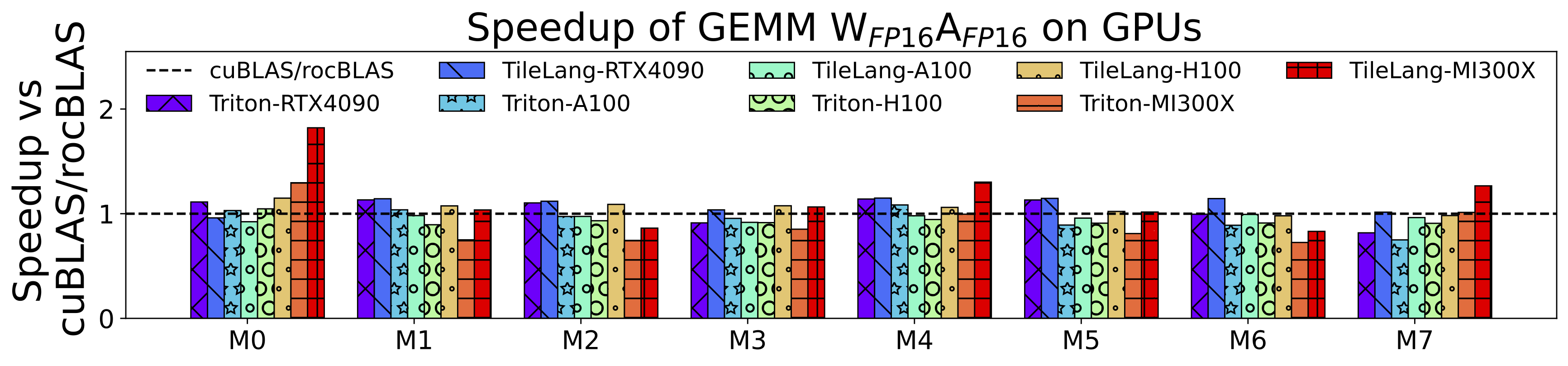
此处的设置具体的设置和复现请看tilelang-benchmark。RTX 4090、A100、H100 和 MI300X TileLang相较于厂商库的加速比为 1.1x、0.97x、1.0x 和 1.04x 的加速比。相比 Triton，TileLang在这些gpu上的加速比分别为 1.08x、1.03x、1.13x 和 1.25x。

结尾处丢一下triton和tilelang level 2的矩阵乘法代码的对比，看上去tile language还是比较简洁的(, 但是在简洁的基础上，tilelang可以允许用户通过annotate手动控制memory layout，和pipeline，以及将一些代码替换为Level 3的实现，增强了很多灵活性(，虽然现在人手有点捉急，但这是一个计划值得持续维护的项目，欢迎大家关注一下中国玩家自己的triton :) https://github.com/tile-ai/tilelang