这里记录的是我想从tvm的tensor expression出发,参考一下cutlass efficient gemm的思路,一步一步优化一下GEMM的一些思考和碎碎念,目的是为了理解cutlass优化gemm的思路。
我们使用CUTLASS Profiler来运行一个gemm的运算,并用nsight compute dump下来其运行过程中的一些情况,可以拿到他的一些信息,如grid的大小与block的大小等。比如对于16384的float32类型数据的gemm,cutlass的grid size是(512, 16, 1)-> 8192个block, block size是(256,1,1),一共是2,097,152个线程,因为最后产生C的大小是(16384,16384),所以平均每个thread需要产生128个C的元素,结合这些参数的信息,使用tvm的te进行schedule(其实可以试试tensor ir),最后成功打到了和cublas,cutlass相近的性能。
测试GPU: rtx 3090 24GB
CUDA Version: 11.1
TVM Version: 10.0
代码放在:https://github.com/LeiWang1999/tvm_gpu_gemm
naive gemm 最navie的情况,一个thread处理一个像素点的数据,这里我们选大小为1024的gemm为例子(因为这么做太慢了,大shape要跑很久)
1 2 3 4 5 for m in range 1024 :for n in range 1024 0.0 for k in range 1024 :
对应到tvm的表达式:
1 2 3 4 5 6 7 8 9 1024 "n" )"A" )"B" )0 , l), name="k" )lambda ii, jj: te.sum (A[k, jj] * B[k, ii], axis=k), name="C" )
tvm可以显式的bind thread,例如我们把第一个维度的loop bind到blockIdx.x,第二个维度的loop bind到threadIdx.x,就完成了每个thread计算一个C的像素。
1 2 3 4 5 6 7 8 9 block_x = te.thread_axis("blockIdx.x" )"blockIdx.y" )"threadIdx.x" )"threadIdx.y" )
运行下来的速度是2.xms是cutlass的二十倍左右,生成的cuda kernel如下:
1 2 3 4 5 6 extern "C" __global__ void __launch_bounds__(1024 ) default_function_kernel0 (float * __restrict__ C, float * __restrict__ A, float * __restrict__ B) {int )blockIdx.x) * 1024 ) + ((int )threadIdx.x))] = 0.000000e+00 f;for (int k = 0 ; k < 1024 ; ++k) {int )blockIdx.x) * 1024 ) + ((int )threadIdx.x))] = (C[((((int )blockIdx.x) * 1024 ) + ((int )threadIdx.x))] + (A[((k * 1024 ) + ((int )threadIdx.x))] * B[((k * 1024 ) + ((int )blockIdx.x))]));
Blocked Gemm 分析上述生成的代码,每个thread需要从global memory读取两个数据,A和B,而显然,A和B中的数据都是可以被复用的,这就导致同一个数据被使用了几次,就从global memory中读取了几次,所需要地总的读取Global Memory的次数为 M*N*K*2 次,写M*N次。
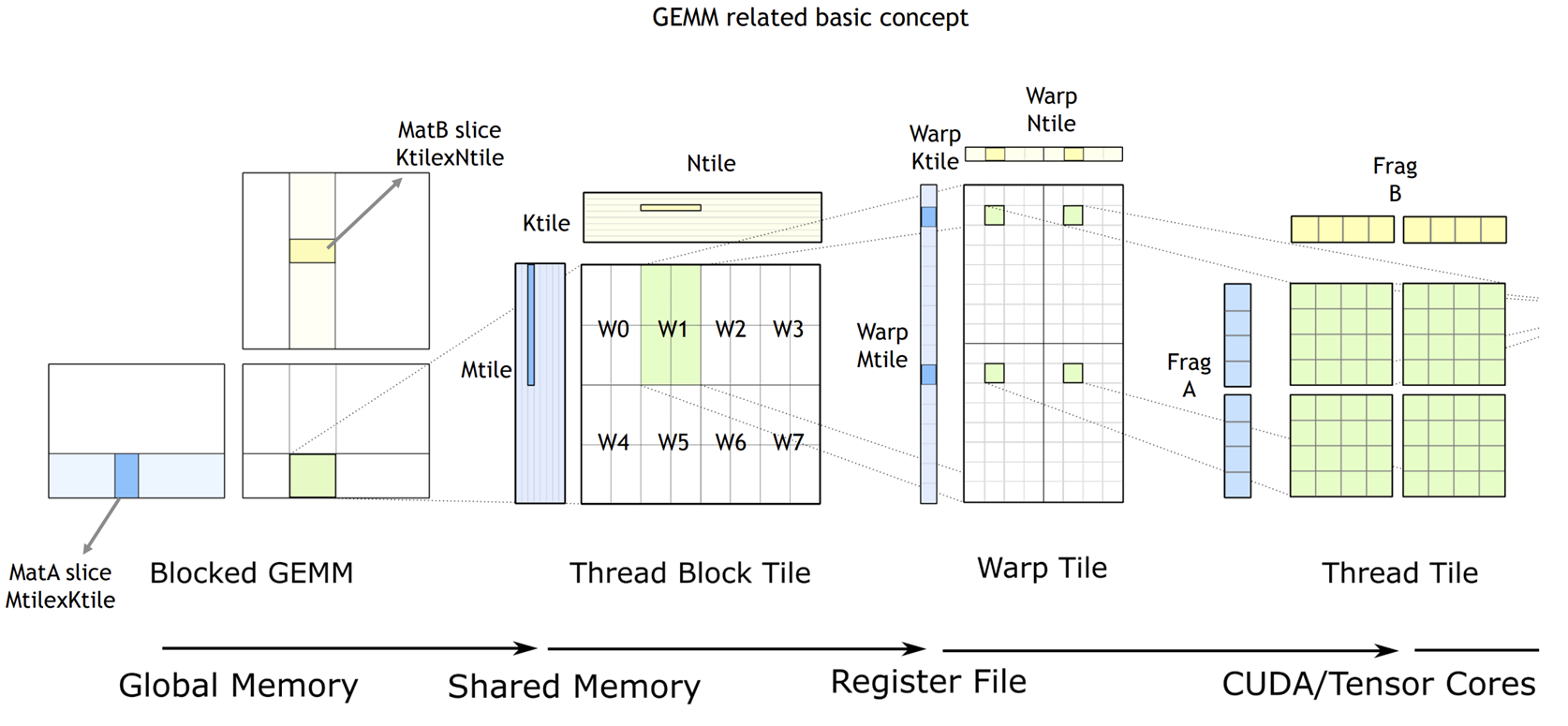
上图是CUTLASS实现高效GEMM的示意图,cutlass在第一层使用矩阵分块的方式来减少global memory的访问次数,在CPU上优化gemm同样也需要用到矩阵分块,不过cpu上的矩阵分块主要是为了fit L2 Cache的大小,这里的却略有不同,cutlass的图描述地不是很明了,绿色的方块代表的是一个block,负责产出一个C子矩阵的数据,可以通过A的浅蓝色的矩阵部分与B的浅黄色的矩阵部分乘累加得到,因为一个block内的thread共享share memory,所以可以提前把这两部分浅色的矩阵cache到share memory中 。
现在暂时不考虑thread block tile这部分内容,则每个block内的thread各自负责一个计算像素,比如,我们一个block负责产生(32,32)个像素则在16384的gemm场景下:
M,K,N: 16384,16384,16384
grid_size: 16384, 16
block_size: 1024 (32,32)
对于grid来说,每一个block需要处理一个小的矩阵,具体到tvm的调度实现代码是:
1 2 3 4 5 6 7 8 9 10 11 12 13 bx, xi = s[C].split(C.op.axis[0 ], factor=(block_h))str (tvm.lower(s, [A, B, C], simple_mode=True )), "progress/2.split_i.cu" )1 ], factor=(block_w))str (tvm.lower(s, [A, B, C], simple_mode=True )), "progress/3.split_j.cu" )str (tvm.lower(s, [A, B, C], simple_mode=True )), "progress/4.bind_block.cu" )str (tvm.lower(s, [A, B, C], simple_mode=True )), "progress/5.bind_thread.cu" )
split一般会用到factor和nparts这两个参数,其中factor指的是拆分因数,及block_h是拆分之后的内循环,nparts是拆成多少份,及指定的参数是拆分之后的外循环。
把i,j两层循环各自拆分成(_, 32),(_, 32), 再将这两层循环外提,就可以达到矩阵分块计算的效果,直接从global memory读取数据进行计算,一次计算的时间是4849.64ms,比cutlass要慢十倍。
接下来,给A、B、C加上cache,先以C举例,”local“表示结果暂存到寄存器中,则数据会先写到CC,再写回global:
1 CC = s.cache_write(C, "local" )
lower:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 @main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()"from_legacy_te_schedule" : True, "global_symbol" : "main" , "tir.noalias" : True}local : Pointer(local float32), float32, [1]), storage_scope = local {local , float32, [1], [], scope="local" , align=4)[0] = 0f32for (k: int32, 0, 16384) {let cse_var_1: int32 = (k*16384)32 )) + threadIdx.y: int32)]*B[((cse_var_1 + (blockIdx.x: int32*32 )) + threadIdx.x: int32)]))"ThreadIndex" , "blockIdx.x" )] "thread_extent" = 512;"ThreadIndex" , "blockIdx.y" )] "thread_extent" = 512;"ThreadIndex" , "threadIdx.x" )] "thread_extent" = 32;"ThreadIndex" , "threadIdx.y" )] "thread_extent" = 32;524288 ) + (threadIdx.x*16384 )) + (blockIdx.y*32)) + threadIdx.y)] = C.local_1[0]
发现计算都在c_local上进行了,但是thread和block都bind在C上,这样直接生成cuda程序会有错误,我们要把c_local挪到C的第一个维度(因为都已经绑定到thread了,所以这里C的计算没有循环,需要绑定到yi。
1 s[CC].compute_at(s[C], yi)
这样可以生成cuda程序,验证性能,不过只把C缓存到local,对性能没有影响,估计是NVCC自己优化掉了,缓存A和B才是关键,但是缓存了A和B,就会尴尬地发现,share memory的大小不够用了,对于每个block,需要load两个16384,32大小的子矩阵,以单精度浮点数为例子,一共是256KB,一个SM也就128KB的share memory资源,所以不可以像这样一个thread计算一个像素。
RTX 3090
register file per SM
256 KB
Maximum number of resident threads per SM
1536
Max number of blocks per SM
16
shared memory size per SM
128 KB
Thread Block Tile 这一步需要进一步的决定,每个block里的thread是怎么计算的,对应cutlass efficent gemm中的第二张图,刚才的方法中,一个thread负责计算一个像素点的数据,在计算数据的时候每个thread又需要从global memory中读取两个 16384, 1 的数据,复用性极差。我们只能再进行分块,一次从global memory中load一部分数据进行计算。
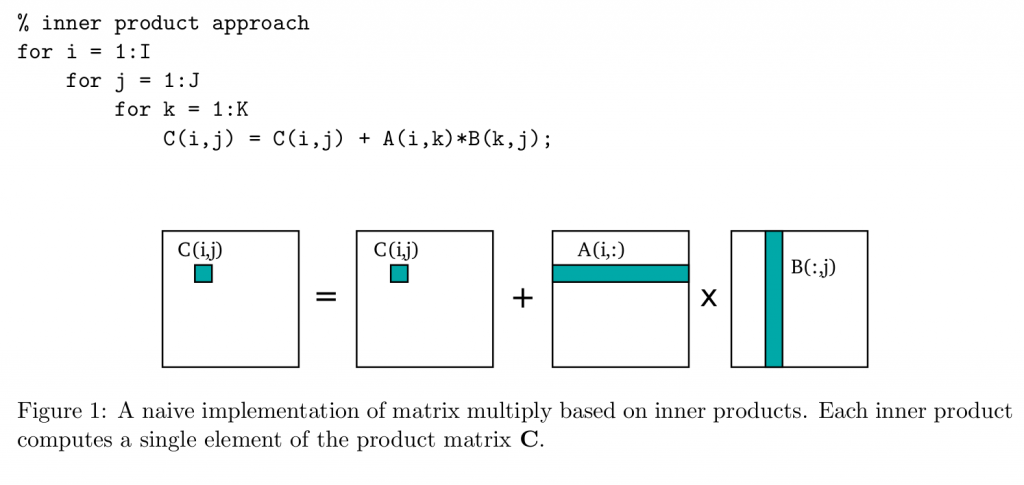
在这之后有两种计算方法,第一种是把浅色部分的矩阵按照inner product的方式,及下图所示:
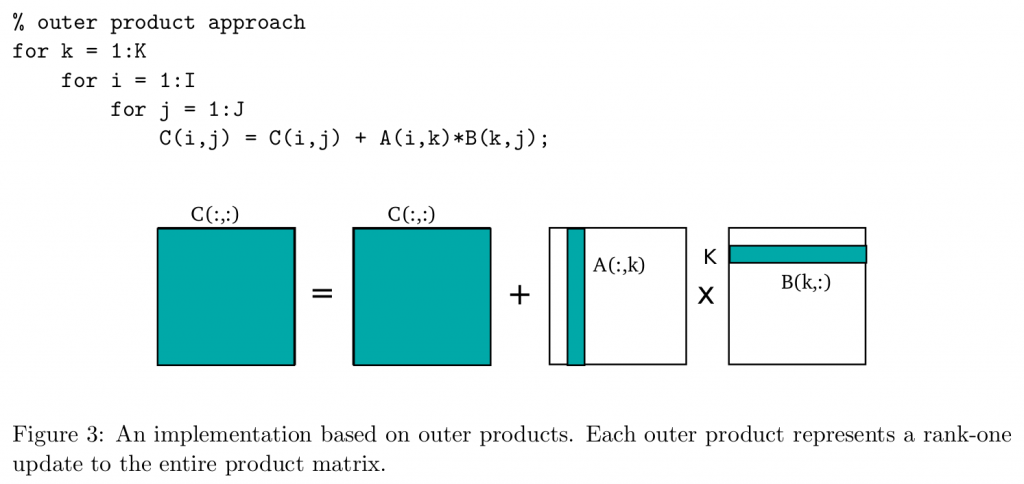
还有一种是outer product,将最内层的K循环提出到最外层:
对应到cutlass的示意图,很明显,我看了很多加速gemm的资料,大家用的都是第二种外积的方式,不过也没有人说为什么要这么用,第一种内积的方式就是把A的浅色矩阵横过来切,我的理解是, 这样算下来有几个不方便的地方,一是外积的方式只需要决定Bk的大小,而外积的方式如果把K固定,那Bm和Bn就有两个参数需要调整,比较麻烦;二是在计算中,总有一些数据会被load多次,造成了额外的访存。虽然这种方式不能缓解inner product的局部性问题,但是在做矩阵分块的时候确实能更好地利用数据,不过外积的方式每次迭代存储的中间结果是一整个矩阵,内积是一小部分矩阵。
More sophisticated algorithms construct the product hierarchically from multiplications of smaller matrix blocks [7]. By computing outer products on small blocks of the input and output matrices, we can more effectively exploit spatial locality and data reuse. Figure 4 illustrates a blocking scheme with parameters I 0, J 0, and K 0.
cite from : https://patterns.eecs.berkeley.edu/?page_id=158
通过这种方式,可以大大缓解之前从global memory获取数据带来的开销,在block计算每个小C矩阵的的时候,需要从global memory读取数据的次数变成了,设小C矩阵的长宽为Bm,Bn, 则总需要的访存量为:b_m + K bn) =MNK(\frac{1}{b_m} + \frac{1}{b_n})
这样,就有几个超参数需要我们确定,Block size需要设置为多大?一个Block计算多少个数据?下面就这个问题讨论一下。
首先,关于block size的大小,一般会有两个具体的限制作约束,Maximum number of resident blocks per SM 和 Maximum number of resident threads per SM,也就是 SM 上最大同时执行的 block 数量和线程数量。要到达这个目的有多种方法,其中一个最简单的方法是让尽量多的线程同时在 SM 上执行,SM 上并发执行的线程数和SM 上最大支持的线程数的比值,被称为 Occupancy,更高的 Occupancy 代表潜在更高的性能。
显然,一个 kernel 的 block_size 应大于 SM 上最大线程数和最大 block 数量的比值,否则就无法达到 100% 的 Occupancy,对应不同的架构,这个比值不相同.>
对于 V100 、 A100、 GTX 1080 Ti 是 2048 / 32 = 64,对于 RTX 3090 是 1536 / 16 = 96,所以为了适配主流架构,如果静态设置 block_size 不应小于 96。虑到 block 调度的原子性,那么 block_size 应为 SM 最大线程数的约数,否则也无法达到 100% 的 Occupancy,主流架构的 GPU 的 SM 最大线程数的公约是 512,96 以上的约数还包括 128 和 256,也就是到目前为止,block_size 的可选值仅剩下 128 / 256 / 512 三个值。
cite from 如何设置CUDA Kernel中的grid_size和block_size?
不难发现,cutlass里的绝大多数kernel都选用的是128和256这两个值,当block中的thread数量变多,单个thread能吃到的资源就变小,反而会对编程产生限制。
其次,关于一个Block计算多少个数据,由于我们已经确定了block的大小,即一个block里可以有128/256个thread,乘上每个thread处理的像素个数,就可以得到每个block要算几个像素了,从刚才得到的公式中可以知道,一个block处理的像素点越多的时候,他的访存量就会越小,但显然这个值是有上限的,一个sm上的thread会均摊share memory。
有大概下面几个约束:
每个block至少需要往share memory里塞 (BM * BK + BK * BN)个数据,如果要乒乓缓存还需要double,一个SM上可以同时处理多个Block(貌似还是碎片化管理,动静态分配结合的方式,所以这也没有一个固定的最大值,可能要用心去感受)。
每个block有最大线程数的限制,如上表所示,3090的一个block的最大线程数是1536。
所以,BM、BN、BK、blockIdx的大小都是可以tune的,这些值确定下来,加上所要处理的所有像素就可以算出grid size。
回归到每个block里的thread是如何计算的,图二一个Block里有1024个线程,包含了八个warp tile,一个warp Tile包含了四个warp,一个warp有32个线程。
对与fp32的cutlass,测了一下在cudacore上最好的square 16384 kernel是cutlass_simt_sgemm_128x128_8x2_nt_align1,grid_size是(1024,16,1),block size是(256,1,1),平均一个线程处理六十四个数据,一个block处理16384个数据。
grid_size是(1024,16,1)和(128,128,1)是否有区别?
两个都是开了16384个 block,可能从thread的角度来看,没什么区别。
我们以同样的尺寸,用tvm模仿一下cutlass,这里我选择grid size是(128,128,1),block size是(16,16,1)。
首先,切一下KTile,这里选择的大小是16,因为我们一个block需要load BK*BN + BM * BK 大小的数据,在这个尺寸下是16128,如果选择BK=8,则是8\ 128, tvm把里面那个thread直接bind到thread会导致有一半的thread不能参与load global memory的任务里来:
1 2 3 4 5 6 BK = 16
对应到生成的代码:
1 2 3 4 5 6 7 8 9 10 11 for (k.outer: int32, 0 , 2048 ) {for (k.inner: int32, 0 , 8 ) {for (ii.c: int32, 0 , 8 ) {for (jj.c: int32, 0 , 8 ) {8 ) + jj.c)64 ) + (k.inner*8 ))
一行有16384个数据,由于BK是8,则每个thread需要迭代2048次才能玩车个完整的C的计算,很正确。
与之前的schedule不一样的是,一个thread需要同时处理多个元素,所以需要首先把loop拆分到threadIdx上:
1 2 3 4 5 bx, xi = s[C].split(C.op.axis[0 ], nparts=Grid_Size_X)1 ], nparts=Grid_Size_Y)
接下来可以把A和B的cache也加上,这下不会out of shared memory了,理一下思路:
在 k.outer 这个维度的迭代中,每次从global memory load BM*BK*BN个数据load到share memory,显然这部分功能可以每个先线程load一部分加快速度。
在k.inner 这个维度的迭代中,把每个thread需要的部分数据load到local(register)上。
所以,我们先把两部分的load放到对应的位置:
1 2 3 4 s[AA].compute_at(s[CC], ko)
对应到生成的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 for (k.outer: int32, 0 , 1024 ) {for (ax0: int32, 0 , 16 ) {for (ax1: int32, 0 , 128 ) {2048 ], [], scope="shared" )[((ax0*128 ) + ax1)] = A[((((k.outer*262144 ) + (ax0*16384 )) + (blockIdx.y*128 )) + ax1)]for (ax0_1: int32, 0 , 16 ) {for (ax1_1: int32, 0 , 128 ) {2048 ], [], scope="shared" )[((ax0_1*128 ) + ax1_1)] = B[((((k.outer*262144 ) + (ax0_1*16384 )) + (blockIdx.x*128 )) + ax1_1)]for (k.inner: int32, 0 , 16 ) {for (ax1_2: int32, 0 , 8 ) {8 ], [], scope="local" , align=32 )[ax1_2] = A.shared_1[(((k.inner*128 ) + (threadIdx.y*8 )) + ax1_2)]for (ax1_3: int32, 0 , 8 ) {8 ], [], scope="local" , align=32 )[ax1_3] = B.shared_1[(((k.inner*128 ) + (threadIdx.x*8 )) + ax1_3)]for (ii.c: int32, 0 , 8 ) {for (jj.c: int32, 0 , 8 ) {8 ) + jj.c)
直接生成cuda kernel运行,一次迭代消耗的时间是13717.8 ms,是cutlass的30倍。
然后,完成读取global memory的并行加速:
1 2 3 4 5 6 7 8 9 10 11 aa_tx, aa_xi = s[AA].split(s[AA].op.axis[0 ], nparts=Block_Size_X)1 ], nparts=Block_Size_Y)0 ], nparts=Block_Size_X)1 ], nparts=Block_Size_Y)
生成的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 for (k.outer: int32, 0 , 1024 ) {for (ax1.inner: int32, 0 , 8 ) {Buffer (A.shared, float32, [2048 ], [], scope="shared" )[(((threadIdx.x*128 ) + (threadIdx.y*8 )) + ax1.inner)] = A[(((((k.outer*262144 ) + (threadIdx.x*16384 )) + (blockIdx.y*128 )) + (threadIdx.y*8 )) + ax1.inner)]for (ax1.inner_1: int32, 0 , 8 ) {Buffer (B.shared, float32, [2048 ], [], scope="shared" )[(((threadIdx.x*128 ) + (threadIdx.y*8 )) + ax1.inner_1)] = B[(((((k.outer*262144 ) + (threadIdx.x*16384 )) + (blockIdx.x*128 )) + (threadIdx.y*8 )) + ax1.inner_1)]for (k.inner: int32, 0 , 16 ) {for (ax1: int32, 0 , 8 ) {Buffer (A.shared.local, float32, [8 ], [], scope="local" , align=32 )[ax1] = A.shared_1[(((k.inner*128 ) + (threadIdx.y*8 )) + ax1)]for (ax1_1: int32, 0 , 8 ) {Buffer (B.shared.local, float32, [8 ], [], scope="local" , align=32 )[ax1_1] = B.shared_1[(((k.inner*128 ) + (threadIdx.x*8 )) + ax1_1)]for (ii.c: int32, 0 , 8 ) {for (jj.c: int32, 0 , 8 ) {8 ) + jj.c)
一次迭代的时间缩小到854ms,已经缩小到cutlass的两倍了!
Wrap Tile & Bank Conflict Shared memory 是以 4 bytes (一个word) 为单位分成 banks:
每个bank的带宽是32 bits per clock cycle
连续的32个word是放在连续的32个banks中
有关bank conflict的内容网上有很多说明的文章,下面是参考这一篇 给出的说明,3090上,一共有32个bank,下面是以16个bank来举例的:
因此,假设以下的数据:
1 __shared__ int data [128];
那么,data[0] 是 bank 0、data[1] 是 bank 1、data[2] 是 bank 2、…、data[15] 是 bank 15,而 data[16] 又回到 bank 0。
由于 warp 在执行时是以 half-warp 的方式执行(关于half-warp参照上一篇博客),因此分属于不同的 half warp 的 threads,不会造成 bank conflict。
因此,如果程序在存取 shared memory的时候,使用以下的方式:
1 int number = data [base + tid];
那就不会有任何 bank conflict,可以达到最高的效率。但是,如果是以下的方式:
1 int number = data [base + 4 * tid];
那么,thread 0 和 thread 4 就会存取到同一个 bank,thread 1 和 thread 5 也是同样,这样就会造成 bank conflict。 在这个例子中,一个 half warp 的 16 个 threads 会有四个 threads 存取同一个 bank,因此存取 share memory 的速度会变成原来的 1/4。
一个重要的例外是,当多个 thread 存取到同一个 shared memory 的地址时,shared memory 可以将这个地址的 32 bits 数据「广播」到所有读取的 threads,因此不会造成 bank conflict。
例如:
这样不会造成 bank conflict,因为所有的 thread 都读取同一个地址的数据。
很多时候 shared memory 的 bank conflict 可以透过修改数据存放的方式来解决。
抱着这个思路回过头来观察我们现在的kernel对share memory的读写:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 for (ax1.inner: int32, 0 , 8 ) {2048 ], [], scope="shared" )[(((threadIdx.x*128 ) + (threadIdx.y*8 )) + ax1.inner)] = A[(((((k.outer*262144 ) + (threadIdx.x*16384 )) + (blockIdx.y*128 )) + (threadIdx.y*8 )) + ax1.inner)]for (ax1.inner_1: int32, 0 , 8 ) {2048 ], [], scope="shared" )[(((threadIdx.x*128 ) + (threadIdx.y*8 )) + ax1.inner_1)] = B[(((((k.outer*262144 ) + (threadIdx.x*16384 )) + (blockIdx.x*128 )) + (threadIdx.y*8 )) + ax1.inner_1)]for (ax1: int32, 0 , 8 ) {8 ], [], scope="local" , align=32 )[ax1] = A.shared_1[(((k.inner*128 ) + (threadIdx.y*8 )) + ax1)]for (ax1_1: int32, 0 , 8 ) {8 ], [], scope="local" , align=32 )[ax1_1] = B.shared_1[(((k.inner*128 ) + (threadIdx.x*8 )) + ax1_1)]
因为float32的长度刚好是一个word,则索引%32就可以作为bank下标的标识。
写的过程中,假设第0个block的第0个thread开始,写入的地址为 0, 8, 16, 24, 32, 40…,明显第一个thread和第五个thread就写入了同一块bank。
thread虽然在逻辑上都是并行处理,但实际上是调度到warp上快速执行完一组thread,再快速执行下一组,而且bank是simd级别的,可以理解为一个share memory controller,所以我们只需要保证同一组warp上的thread不conflict就可以了。
分析之前的程序,写share memory部分造成conflict的原因主要是写schedule的时候,没有把最后一层的loop拆成threadx导致的,重新改一下schedule:
1 2 3 4 5 6 7 8 9 10 11 aa_yi, aa_ty = s[AA].split(s[AA].op.axis[0 ], factor=Block_Size_Y)1 ], factor=Block_Size_X)0 ], factor=Block_Size_Y)1 ], factor=Block_Size_X)
生成的代码:
1 2 3 4 5 6 for (int ax1_outer = 0 ; ax1_outer < 8 ; ++ax1_outer) {int )threadIdx.y) * 128 ) + (ax1_outer * 16 )) + ((int )threadIdx.x))] = A[(((((k_outer * 262144 ) + (((int )threadIdx.y) * 16384 )) + (((int )blockIdx.y) * 128 )) + (ax1_outer * 16 )) + ((int )threadIdx.x))];for (int ax1_outer1 = 0 ; ax1_outer1 < 8 ; ++ax1_outer1) {int )threadIdx.x) * 128 ) + (ax1_outer1 * 16 )) + ((int )threadIdx.y))] = B[(((((k_outer * 262144 ) + (((int )threadIdx.x) * 16384 )) + (((int )blockIdx.x) * 128 )) + (ax1_outer1 * 16 )) + ((int )threadIdx.y))];
可以发现变成 s[tid] = g[xx]的形式了,没有bank conflict,而运行的时间也快了一些(快了100ms 左右的样子)。
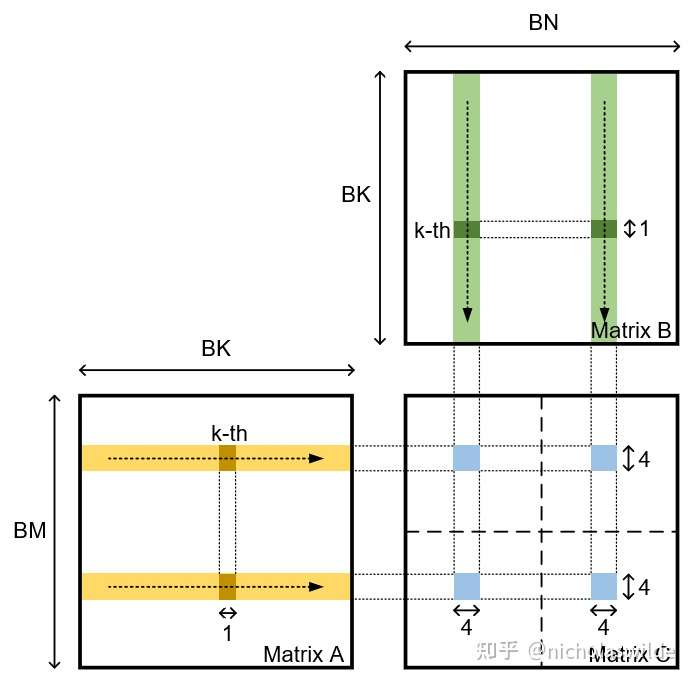
显然读的过程也存在bank conflict,这一点可以从第三张图中看到,左上角的32个虚线方格是一个warp的32个thread,同一行的thread会同时读取同一个A的值,同一列的thread会同时读取一个B的值,而从图中也能看出cutlass是怎么缓解这个问题:
访存的地址是:
1 2 3 4 5 6 for (int ax1 = 0 ; ax1 < 8 ; ++ax1) {128 ) + (((int )threadIdx.y) * 8 )) + ax1)];for (int ax11 = 0 ; ax11 < 8 ; ++ax11) {128 ) + (((int )threadIdx.x) * 8 )) + ax11)];
对于A来说,前十六个thread访问的memory地址是一样的,但是这时候应该有broadcast,对于B来说,访问的地址是0,8,16,32(32的时候会有conflict),
之前有人已经给出更丰富的图片说明了:https://zhuanlan.zhihu.com/p/518857175
在tvm里,实现这样的切分方式,并且明确说明了目的是为了缓解bank conflict的是virtual thread,如下:
1 2 3 4 5 6 7 8 tyz, yi = s[C].split(yi, nparts=2 )8 )
565ms,生成的代码是:
1 2 3 4 5 6 7 8 B.shared.local_1: Buffer(B.shared.local, float32, [1 ], [], scope="local" , align=4 )[0 ] = B.shared_1[((k.inner*128 ) + threadIdx.x)]1 ] = B.shared_1[(((k.inner*128 ) + threadIdx.x) + 16 )]2 ] = B.shared_1[(((k.inner*128 ) + threadIdx.x) + 32 )]3 ] = B.shared_1[(((k.inner*128 ) + threadIdx.x) + 48 )]4 ] = B.shared_1[(((k.inner*128 ) + threadIdx.x) + 64 )]5 ] = B.shared_1[(((k.inner*128 ) + threadIdx.x) + 80 )]6 ] = B.shared_1[(((k.inner*128 ) + threadIdx.x) + 96 )]7 ] = B.shared_1[(((k.inner*128 ) + threadIdx.x) + 112 )]
这样,就没有bank conflict了,vthread虽然是虚拟的,但是如果直接用split+reorder的方式来替换:
1 2 3 4 5 6 7 tyz, yi = s[C].split(yi, nparts=2 )2 )
速度反而会慢不少(692.994ms),也有人在论坛里讨论过 ,而且看tvm的论文里提到的vthread,似乎还有类似于分析依赖,软件流水的神奇功能。
其他 vectorize 从global memory读取数据可以使用lgd.128指令,一次读4个float32的数据,从share memory 读取数据,可以用lgs.128,对应到tvm里则是使用vectorize进行向量化,这样,一条访存指令就可以直接load 4个float32的数据,为了做到这一点,首先需要从循环中把可以vectorize的shape手动拆出来,再进行向量化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 aa_yi, aa_ty = s[AA].split(s[AA].op.axis[0 ], factor=Block_Size_Y)1 ], factor=Block_Size_X * 4 )0 ], factor=Block_Size_Y)1 ], factor=Block_Size_X * 4 )
生成的代码:
1 2 3 4 5 6 for (int ax1_outer = 0 ; ax1_outer < 2 ; ++ax1_outer) {int )threadIdx.y) * 128 ) + (ax1_outer * 64 )) + (((int )threadIdx.x) * 4 ))) = *(float4*)(A + (((((k_outer * 262144 ) + (((int )threadIdx.y) * 16384 )) + (((int )blockIdx.y) * 128 )) + (ax1_outer * 64 )) + (((int )threadIdx.x) * 4 )));for (int ax1_outer1 = 0 ; ax1_outer1 < 2 ; ++ax1_outer1) {int )threadIdx.y) * 128 ) + (ax1_outer1 * 64 )) + (((int )threadIdx.x) * 4 ))) = *(float4*)(B + (((((k_outer * 262144 ) + (((int )threadIdx.y) * 16384 )) + (((int )blockIdx.x) * 128 )) + (ax1_outer1 * 64 )) + (((int )threadIdx.x) * 4 )));
514ms,又快了50ms,接下来还可以对local register的访问做vectorize,也可以用lds.128,所以需要把vthread的大小改成2x2,这样分出来刚好是两个可以被vectorize的向量:
1 2 3 4 5 6 7 8 9 tyz, yi = s[C].split(yi, nparts=2 )2 )
生成的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 __shared__ float4 A_shared[512 ];512 ]; for (int k_inner = 0 ; k_inner < 16 ; ++k_inner) {0 ) = A_shared[((k_inner * 32 ) + ((int )threadIdx.y))];4 ) = A_shared[(((k_inner * 32 ) + ((int )threadIdx.y)) + 16 )];0 ) = B_shared[((k_inner * 32 ) + ((int )threadIdx.x))];4 ) = B_shared[(((k_inner * 32 ) + ((int )threadIdx.x)) + 16 )];for (int ii_c = 0 ; ii_c < 4 ; ++ii_c) {for (int jj_c = 0 ; jj_c < 4 ; ++jj_c) {4 ) + jj_c)] = (C_local[((ii_c * 4 ) + jj_c)] + (A_shared_local[jj_c] * B_shared_local[ii_c]));4 ) + jj_c) + 32 )] = (C_local[(((ii_c * 4 ) + jj_c) + 32 )] + (A_shared_local[(jj_c + 4 )] * B_shared_local[ii_c]));4 ) + jj_c) + 16 )] = (C_local[(((ii_c * 4 ) + jj_c) + 16 )] + (A_shared_local[jj_c] * B_shared_local[(ii_c + 4 )]));4 ) + jj_c) + 48 )] = (C_local[(((ii_c * 4 ) + jj_c) + 48 )] + (A_shared_local[(jj_c + 4 )] * B_shared_local[(ii_c + 4 )]));
这样,一个warp里的thread访问的bank就是0,4,8,12,16…32. 到第九个线程的时候还是会出现bank conflict?这个应该是无法避免了,可能得交给nvcc来做软件流水,但是速度确实快了不少,达到了423ms, cublas和cutlass测出来的结果都是420ms,已经基本上达到这个水平了!
double buffer 当然如果load的时间过长,计算不能hide load latency的时候,可以试试double buffer来进行乒乓缓存,不过占用的share memory会翻倍,直接:
1 2 s[AA].double_buffer()
但是在我的case下面,这个操作加上反而变得更慢(430ms)。。
最后 都已经能打到和cutlass相同的水平,我觉得也就差不多了,至少验证了tvm是真的行(至少在gemm上),当然以上有一些我自己的思考,不一定对,文章里还有一些问题没有解决,比如,(1024,16,1)和(128,128,1)这两个grid size是一样的么?群友觉得是不一样的,而我图编程方便,使用的后者,cutlass用的是前者,但从结果上来看,效果还可以,关于这些,欢迎大佬指正与交流,至于前面的区域,以后有时间了再来探索吧。



Comments