tvm storage align

回答知乎提问：https://www.zhihu.com/question/565420155

最近正好研究了一下这个schedule，顺便简单总结一下，官方给的文档介绍确实比较抽象: https://tvm.apache.org/docs/reference/api/python/tir.html

题主困惑的应该是factor和offset是什么意思，为什么这样能够解决shared memory bank conflict？

第一个问题，可以看看代码，首先是底层的实现(https://github.com/apache/tvm/blob/HEAD/src/tir/transforms/storage_flatten.cc#L480-L481)：

PrimExpr stride = make_const(shape[first_dim].dtype(), 1);
for (size_t i = shape.size(); i != 0; --i) {
  size_t dim = i - 1;
  if (dim < avec.size() && avec[dim].align_factor != 0) {
    PrimExpr factor = make_const(stride.dtype(), avec[dim].align_factor);
    PrimExpr offset = make_const(stride.dtype(), avec[dim].align_offset);
    stride = stride + indexmod(factor + offset - indexmod(stride, factor), factor);
    stride = bound_analyzer_->Simplify(stride);
  }
  rstrides.push_back(stride);
  stride = stride * shape[dim];
}

显然可以通过图中的公式计算出最后的stride，例如网上能搜到的一个case:

import tvm

n = 1024
factor = 100
offset = 8
dtype = "float32"
A = tvm.te.placeholder((n, n), dtype=dtype, name='A')
k = tvm.te.reduce_axis((0, n), name='k')
B = tvm.te.compute((n,), lambda i: tvm.te.sum(A[i, k], axis=k), name='B')

s = tvm.te.create_schedule(B.op)
AA = s.cache_read(A, "shared", [B])

print(tvm.lower(s, [A, B], simple_mode=True))
print("---------cutting line---------")

s[AA].storage_align(AA.op.axis[0], factor, offset)

print(tvm.lower(s, [A, B], simple_mode=True))

'''
@main = primfn(A_1: handle, B_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1024], [])}
  buffer_map = {A_1: A, B_1: B}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024], [])} {
  allocate(A.shared: Pointer(shared float32), float32, [1048576]), storage_scope = shared {
    for (ax0: int32, 0, 1024) {
      for (ax1: int32, 0, 1024) {
        let cse_var_1: int32 = ((ax0*1024) + ax1)
        A.shared_1: Buffer(A.shared, float32, [1048576], [], scope="shared")[cse_var_1] = A[cse_var_1]
      }
    }
    for (i: int32, 0, 1024) {
      B[i] = 0f32
      for (k: int32, 0, 1024) {
        B[i] = (B[i] + A.shared_1[((i*1024) + k)])
      }
    }
  }
}


---------cutting line---------
@main = primfn(A_1: handle, B_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1024], [])}
  buffer_map = {A_1: A, B_1: B}
  preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024], [])} {
  allocate(A.shared: Pointer(shared float32), float32, [1134592]), storage_scope = shared {
    for (ax0: int32, 0, 1024) {
      for (ax1: int32, 0, 1024) {
        A.shared_1: Buffer(A.shared, float32, [1134592], [], scope="shared")[((ax0*1108) + ax1)] = A[((ax0*1024) + ax1)]
      }
    }
    for (i: int32, 0, 1024) {
      B[i] = 0f32
      for (k: int32, 0, 1024) {
        B[i] = (B[i] + A.shared_1[((i*1108) + k)])
      }
    }
  }
}
'''

用这个公式计算一下：
$$
(100+8-1024%100)% 100 + 1024 = (108-24) + 1024 = 1108
$$
这个公式可以理解为，对于原来给定的一个stride，如1024，首先跟factor对其，如1024对其之后是1100，再补上offset，可以实现一个类似memory zero padding的效果，再tvm的repo里，还可以翻到一些经常用的(并没有，奇怪的用法：

s[CS].storage_align(bb, CS_align - 1, CS_align)

推导一下公式
$$
stride = stride + (C-1+C-(stride%(C-1)))% (C-1)
$$
而在一些情况下, 这里的CS_align等于stride,则stride不变,如果加上一个offset,则需要另外考虑。

第二个问题需要了解一下在gpu矩阵乘法计算中的一种通过加pad的方式解决bank conflict的方法，假设我们都按照cutlass的思路来进行矩阵乘法计算，并且利用tensorcore，以一个简单的warp算m16n16k16的矩阵乘法为例子：

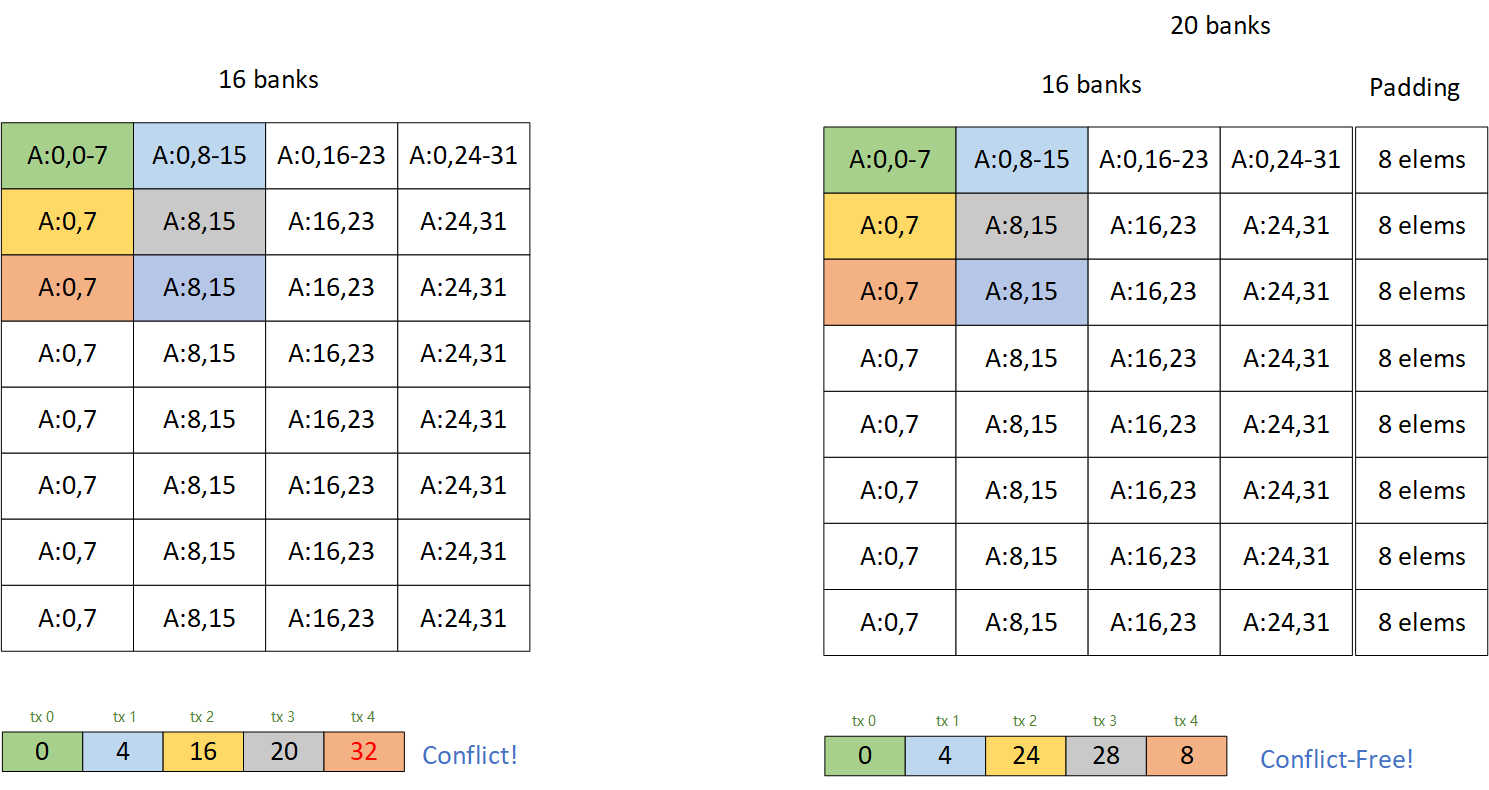
左边图片中白色的部分是一个典型的A矩阵在shared memory里的排布，大小是128*32的矩阵，一次取一个小矩阵在内存的排布，一次使用l ds128指令取八个float16的元素，每个线程访问的bank如下面所示，有一半的bank是没有被访问到的，一种常用的解法是给每一行加PAD，例如右图，每一行加4个bank大小的pad，这样带宽就可以利用满，这样做法的优点是简单，但是缺点也很明显，一是写入shared memory就会有conflict，需要动脑消除一下，二是会增加shared memory的开销，有了这个图示，就可以解决第二个问题了。

回到tvm，如果只用一个storage align schedule，速度可能会快一些，这来源于你解决了wmma::load_matrix_sync引入的shared memory load conflict，但是因为从global memory读入shared memory的shared memory store过程中线程与线程之间多了padding，会导致引入store的conflict。

而且理论上存在解，不需要加padding，控制好每个线程访问的bank让他们不conflict，cutlass里提供了这样的一种解法：

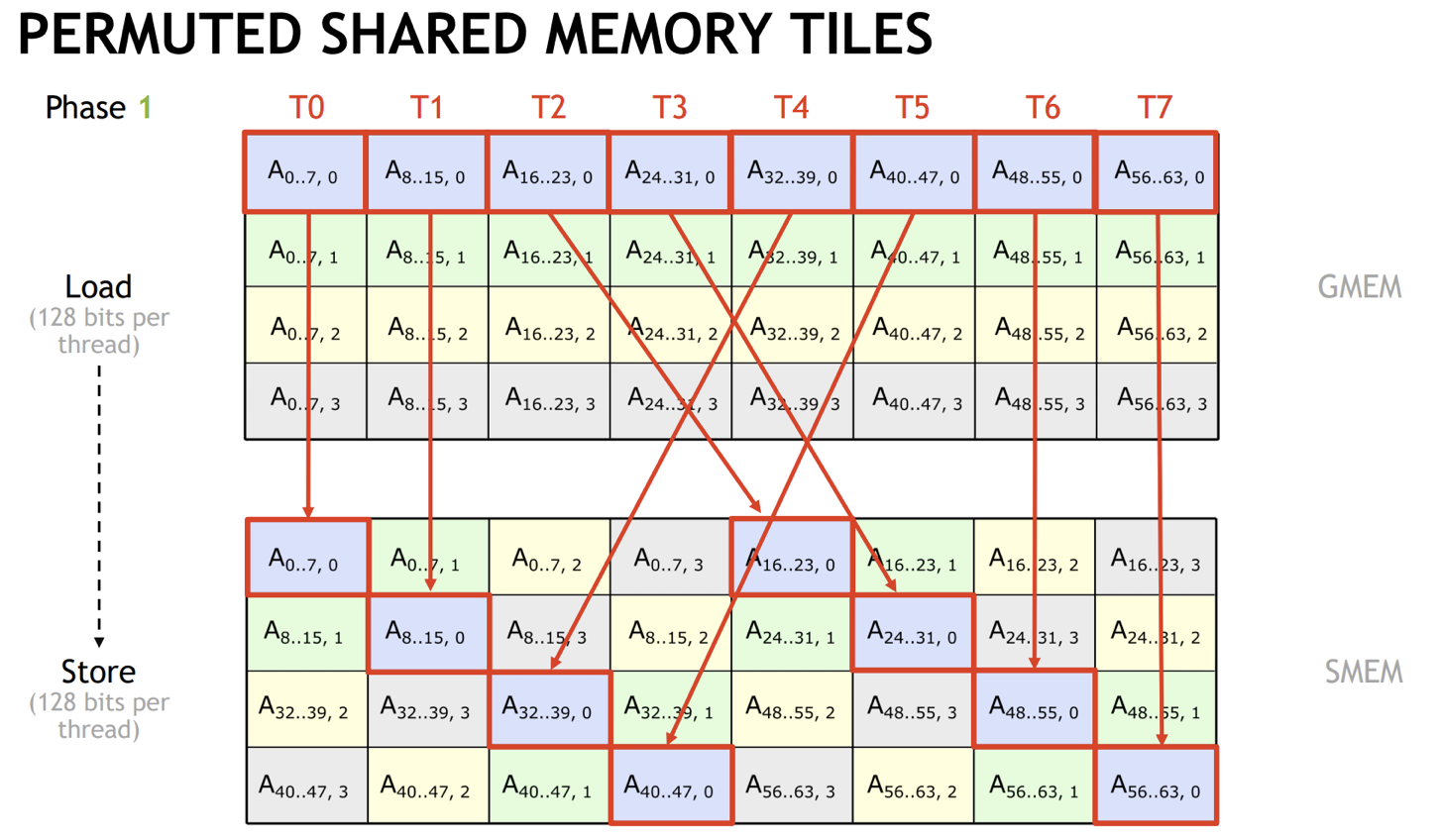
这两种情况显然不能用storage_align解决了，可以用tvm的tensorize schdule和decl_buffer来达到这个目的，这种实现方式也更自由，如这里的代码：

import tvm
from tvm import te

def intrin_load_matrix_to_slb():
    output_shape = (16, 64)
    strides_src = [64, 1]
    strides_dst = [64, 1]

    A = te.placeholder(output_shape, name="A", dtype="float32")
    C = te.compute(output_shape, lambda *i: A(*i), name="C")

    BA = tvm.tir.decl_buffer(A.shape, A.dtype, scope="global", strides=strides_src, data_alignment=64, offset_factor=1)
    BC = tvm.tir.decl_buffer(C.shape, C.dtype, scope="shared",  strides=strides_dst, data_alignment=64, offset_factor=1)

    def intrin_func(ins, outs):
        ib = tvm.tir.ir_builder.create()

        BA = ins[0]
        BC = outs[0]

        tx = te.thread_axis("threadIdx.x")
        ib.scope_attr(tx, "thread_extent", 64)
        index = tx // 1

        for outer in range(0, 16):
                ib.emit(BC.vstore([outer, index], BA.vload([outer, index], "float32")))

        return ib.get()
    return te.decl_tensor_intrin(C.op, intrin_func, binds={A: BA, C: BC})

M = 64
N = 64
A = te.placeholder((M, N), dtype="float32", name="A")
B = te.compute((M, N), lambda *i: A(*i), name="B", )
s = te.create_schedule(B.op)
tx = te.thread_axis("threadIdx.x")
AS = s.cache_read(A, "shared", [B])
cx, ci = B.op.axis
cxo, cxi = s[B].split(cx, factor=16)
s[B].reorder(cxo, cxi, ci)
s[B].bind(ci, tx)

s[AS].compute_at(s[B], cxo)
ax, ai = AS.op.axis
# s[AS].storage_align(ax, 63, 64)
s[AS].tensorize(ax, intrin_load_matrix_to_slb())
s[AS].double_buffer()
print(tvm.lower(s, [A, B]))

output:
  @main = primfn(A_1: handle, B_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {B: Buffer(B_2: Pointer(float32), float32, [64, 64], []),
             A: Buffer(A_2: Pointer(float32), float32, [64, 64], [])}
  buffer_map = {A_1: A, B_1: B} {
  allocate(A.shared: Pointer(shared float32), float32, [1024]), storage_scope = shared;
  for (i0.outer: int32, 0, 4) {
    attr [IterVar(threadIdx.x: int32, (nullptr), "ThreadIndex", "threadIdx.x")] "thread_extent" = 64 {
      A.shared[threadIdx.x] = (float32*)A_2[((i0.outer*1024) + threadIdx.x)]
      A.shared[(threadIdx.x + 64)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 64)]
      A.shared[(threadIdx.x + 128)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 128)]
      A.shared[(threadIdx.x + 192)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 192)]
      A.shared[(threadIdx.x + 256)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 256)]
      A.shared[(threadIdx.x + 320)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 320)]
      A.shared[(threadIdx.x + 384)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 384)]
      A.shared[(threadIdx.x + 448)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 448)]
      A.shared[(threadIdx.x + 512)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 512)]
      A.shared[(threadIdx.x + 576)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 576)]
      A.shared[(threadIdx.x + 640)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 640)]
      A.shared[(threadIdx.x + 704)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 704)]
      A.shared[(threadIdx.x + 768)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 768)]
      A.shared[(threadIdx.x + 832)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 832)]
      A.shared[(threadIdx.x + 896)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 896)]
      A.shared[(threadIdx.x + 960)] = (float32*)A_2[(((i0.outer*1024) + threadIdx.x) + 960)]
    }
    for (i0.inner: int32, 0, 16) {
      attr [IterVar(threadIdx.x_1: int32, (nullptr), "ThreadIndex", "threadIdx.x")] "thread_extent" = 64;
      B_2[(((i0.outer*1024) + (i0.inner*64)) + threadIdx.x_1)] = (float32*)A.shared[((i0.inner*64) + threadIdx.x_1)]
    }
  }
}