之前回答某个知乎问题的时候简单描述了一下为什么通过加padding的方式可以解bank conflict:
https://www.zhihu.com/question/565420155
当时我画了这样一个图片:
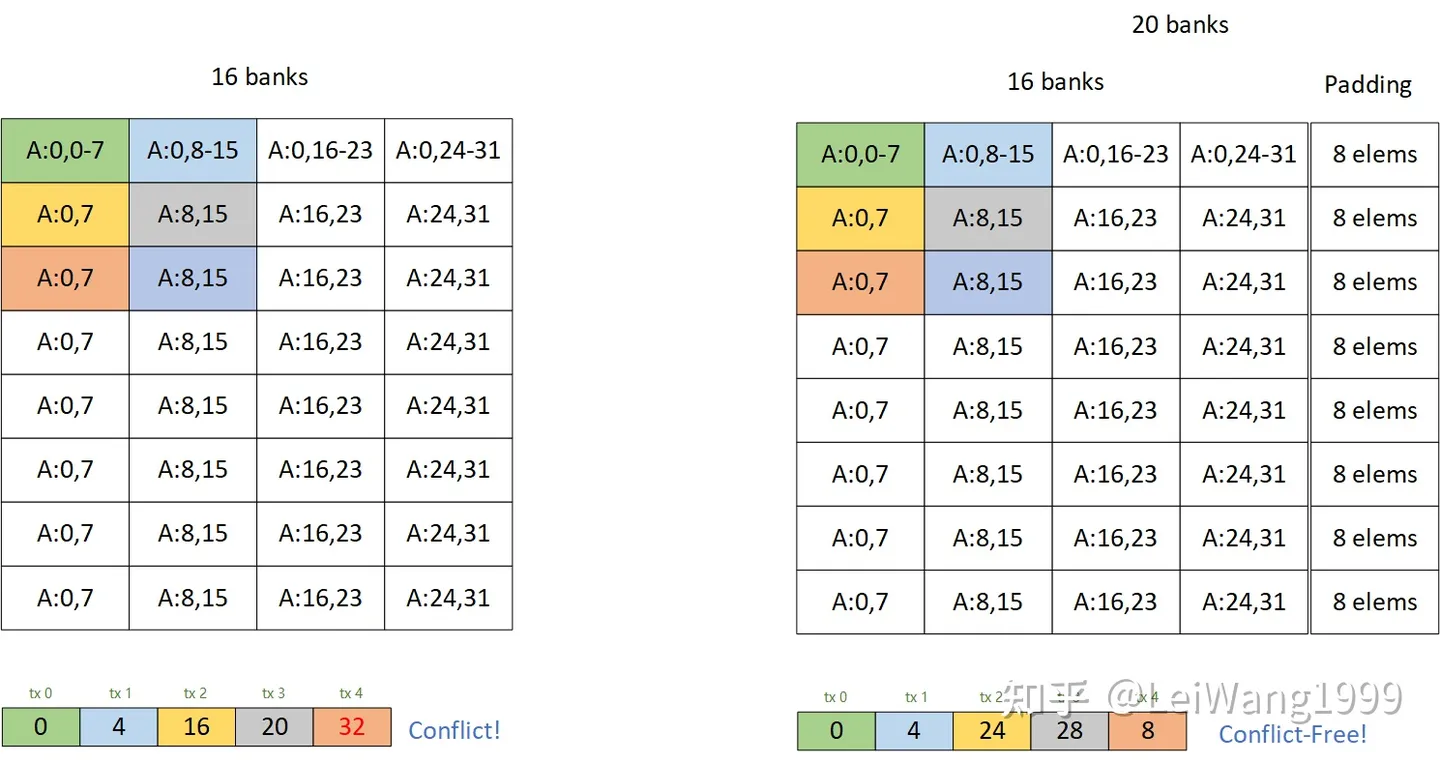
有一些同学还是不理解为什么这种方式可以解掉bank conflict,再加上我搜一搜也没发现有人讲清楚过这件事情。这篇文章以利用tensor core的矩阵乘法为例,较详细地分析一下解conflict的方法,同样我们选择一个最典型的cutlass tile 128x256x32 的 float16 的tile,用来说明问题,在最后,我会提供一份复现的代码,由Tensor IR实现,方便实现各种Tile(虽然我觉得加pad的性能并不能足够到sota。
当pad不存在的时候
以A矩阵的第一个Block的第一个bk为例,我们需要把global memory左上角的128x32的矩阵缓存到shared memory,这部分只需要最简单的线程映射就可以做到conflict free shared memory store, 然后我们对这个128x32的矩阵使用16x16x16的wmma指令计算,使用8个warp的话,按照2x4的分法来分,一个线程需要算64x64大小的矩阵,一共需要4x4个mma_sync,因为BK=32,wmma_k=16,所以一共需要8条shared memory load指令。
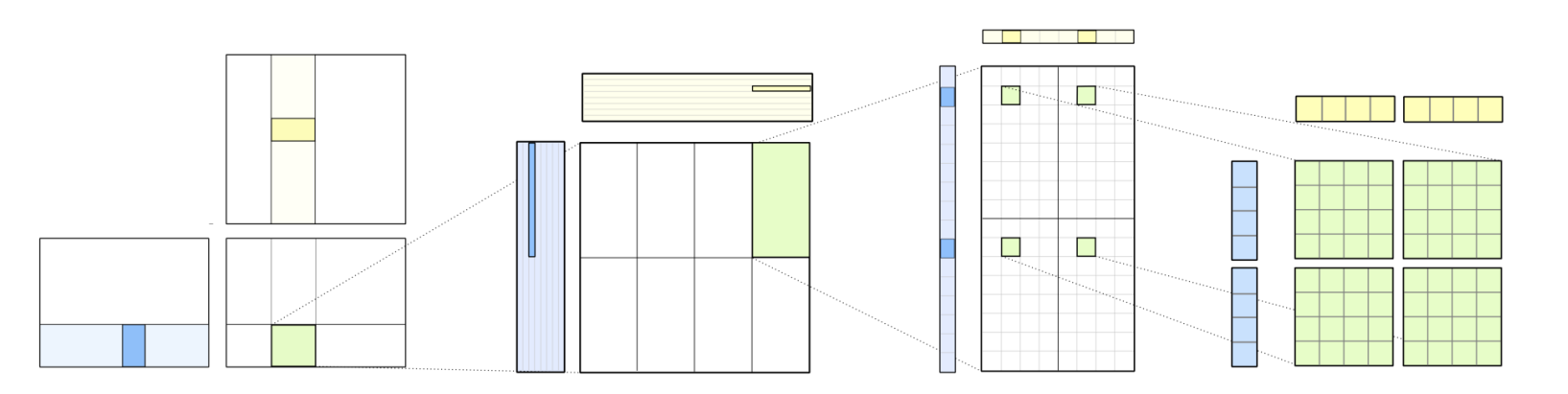
不过上面那一段的分析都不重要,我们只需要知道,一个warp会一起来计算一个16x16x16的矩阵乘法,而bank conflict也是warp level,例如该图:
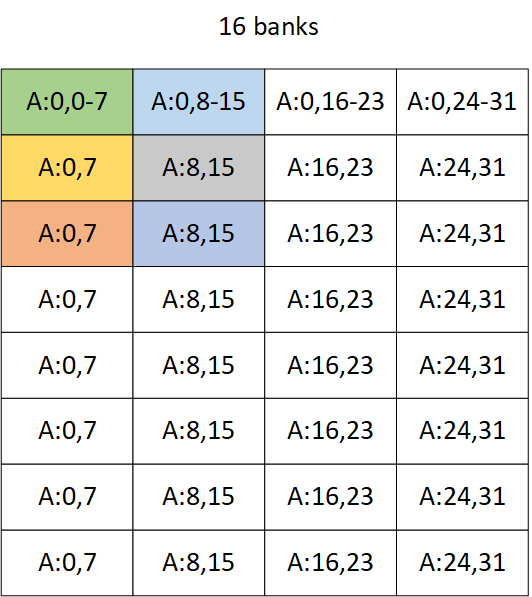
第一个warp的第一个计算需要取到128x32的左上角的16x16大小的数据,这里暂且不说每个线程是如何取数据,不难发现肯定有一半的带宽是浪费掉的,因为一行刚好是16个bank,左半边的数据只能吃到前8个bank,自然会有conflict,我们丢到nsight system里prof一下,结果符合我们的预期:
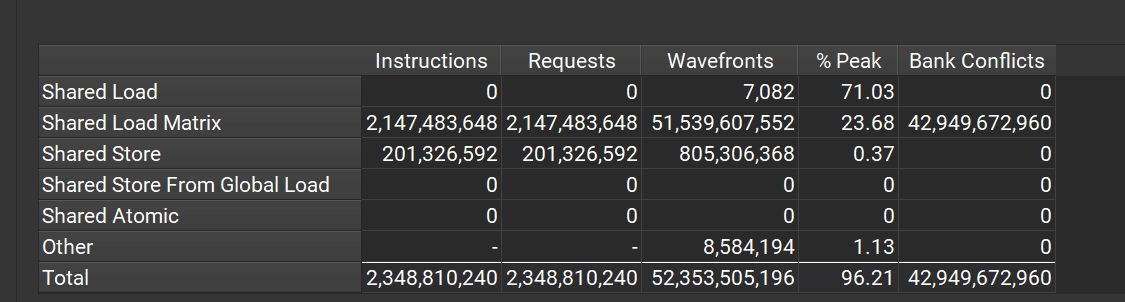
每行加上padding之后
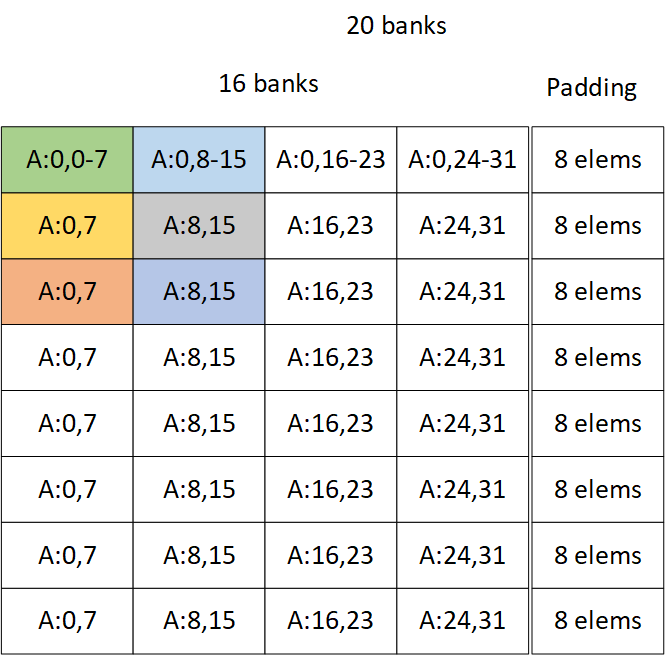
加pad,及在每一行补上几个元素,比如补8个元素,这样每一行就会有20个bank,左边的16x16的矩阵理论上就可以拿到所有的bank,不会出现带宽的浪费。但是,这还需要具体到每个线程需要取哪个bank上的数据,才能够理解明白这件事情。
但是WMMA的API又是一个黑盒子,你看不到它具体的实现,于是这里我们用MMA指令来模拟一下WMMA。
比如说,在我的3090上,float16精度的wmma最后会被翻译成若干个 m16n8k8大小的mma ptx指令,而m16n8k8的指令需要每个线程取这些地址上的数据:

而因为wmma的大小是16x16,这条指令只能算16x8,所以他需要由两个m16n8k8横着排来算,这样每个线程要取哪个地址上的数据就很清晰了,比如线程0,需要取的数据是 (0, 01), (0, 89), (8, 01), (8, 89),具体分析一个warp取到的bank数,那就是:
| thread idx | total bank | inner bank |
|---|---|---|
| 0~3 | 0~3 | 0~3 |
| 4~7 | 20~23 | 20~23 |
| 8~11 | 40~43 | 8~11 |
| 12~15 | 60~63 | 28~31 |
| 16~19 | 80~83 | 16~19 |
| 20~23 | 100~103 | 4~7 |
| 24~27 | 120~123 | 24~27 |
| 28~31 | 140~143 | 12~15 |
刚好是conflict free! 非常巧妙,这个时候我们再prof一下:
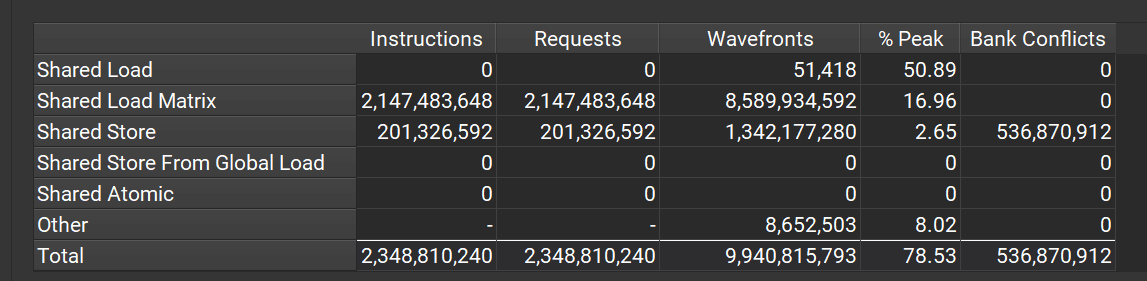
可以看到,shared load matrix这个conflict已经完全消除了,但是却又引入了shared store conflict.
大家可能会关心两个问题:
为什么会产生该conflict?
因为从global 存储到shared memory的过程中,每一行之间多了四个空出来的bank,导致每一行都会跳过4个bank,引入了conflict,而且这个conflict非常难解绝。
为什么加上padding之后性能会有显著的提升?
因为从kernel角度看,load的次数是store的若干倍,解掉的conflict已经远大于引入的conflict,从而带来了性能上的收益。
如果在一些io比巨大的kernel里,这么一点conflict也不太重要,往往一些这样解出来之后效果也可以和cublas达到差不多的效果,但是一般不能到sota。
怎样做到conflict free呢?
观察sota的库,例如cublas/cutlass的gemm kernel,可以看到他的shared memory刚好满足tile和software pipeline的乘积,由此可见其是没有用到padding求解的,而是采用一种更高明,更复杂的permutation机制,精心控制每个数据存储的位置达到最好的带宽利用,比如fp32可以用对角线存储,对应到tensor core也有一些巨无敌复杂的公式,很让人头秃,不过这都是后话了。
Comments